题目内容
在Rt△ABC中，CD、CE分别是斜边AB上的高和中线，且该图中共有x个三角形与△ABC相似，则x=（ ）
分析：利用直角三角形的性质和同角的余角相等，可证出Rt△ABC∽Rt△ACD，且Rt△ABC∽Rt△CBD．再根据∠DCE不确定，随AC、BC的比值变化而变化，得到Rt△DCE与Rt△ABC不一定相似，可得x=2．
解答：解：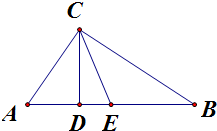
∵Rt△ABC中，∠ACB=90°，CD⊥AB
∴∠ACD=90°-∠A=∠B，
因此Rt△ABC∽Rt△ACD，
同理可得：Rt△ABC∽Rt△CBD，
得到与△ABC相似的三角形有△ACD、△CBD两个
又∵∠DCE不确定，随AC、BC的比值变化而变化
∴Rt△DCE与Rt△ABC不一定相似
综上，若图中共有x个三角形与△ABC相似，则x=2
故选：C
∵Rt△ABC中，∠ACB=90°，CD⊥AB∴∠ACD=90°-∠A=∠B，
因此Rt△ABC∽Rt△ACD，
同理可得：Rt△ABC∽Rt△CBD，
得到与△ABC相似的三角形有△ACD、△CBD两个
又∵∠DCE不确定，随AC、BC的比值变化而变化
∴Rt△DCE与Rt△ABC不一定相似
综上，若图中共有x个三角形与△ABC相似，则x=2
故选：C
点评：本题给出Rt△ABC斜边上的中线与高，求图中与Rt△ABC相似的三角形的个数，着重考查了直角三角形的性质和同角的余角相等的知识，属于基础题．
练习册系列答案
相关题目
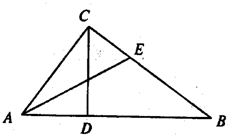如图，在Rt△ABC中，∠C是直角，AC=3，BC=4，CD⊥AB于点D，∠A的平分线交CD于点M，交BC于点E，求：
如图1，在Rt△ABC中，∠C=90°，BC=3，AC=6．D、E分别是AC、AB上的点，且DE∥BC，将△ADE沿DE折起到△A1DE的位置，使A1D⊥CD，如图2．
选修4-1：几何证明选讲