题目内容
已知函数 (其中x∈R,A>0,ω>0)的最大值为2,最小正周期为8.
(其中x∈R,A>0,ω>0)的最大值为2,最小正周期为8.
(1)求函数f(x)的解析式;
(2)若函数f(x)图象上的两点P,Q的横坐标依次为2,4,O为坐标原点,求△POQ的面积.
(1)解:∵f(x)的最大值为2,且A>0,∴A=2.…(1分)
∵f(x)的最小正周期为8,∴ ,得
,得 .…(2分)
.…(2分)
∴f(x)=2sin( x+
x+ ).…(3分)
).…(3分)
(2)解法1:∵ ,…(4分)
,…(4分)
∴ ,…(5分)
,…(5分)
∴ .
.
∴ .…(8分)
.…(8分)
∴ .…(10分)
.…(10分)
∴ =
= .…(11分)
.…(11分)
∴△POQ的面积为 =
= .…(12分)
.…(12分)
解法2:∵ ,…(4分)
,…(4分)
∴ ,…(5分)
,…(5分)
∴ .
.
∴直线OP的方程为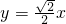 ,即
,即 .…(7分)
.…(7分)
∴点Q到直线OP的距离为 .…(9分)
.…(9分)
∵ ,…(11分)
,…(11分)
∴△POQ的面积为 =
= .…(12分)
.…(12分)
分析:(1)由函数的最大值求出A,由周期求得ω,从而求得函数的解析式.
(2)解法1:先求出P、Q两点的坐标,利用两个向量的夹角公式求得cos∠POQ,可得sin∠POQ的值,根据△POQ的面积为 ,运算求得结果.
,运算求得结果.
解法2:先求出P、Q两点的坐标,利用点到直线的距离公式求得点Q到直线OP的距离d以及OP的长度,再根据△POQ的面积为 运算求得结果.
运算求得结果.
点评:本小题主要考查三角函数的图象与性质、诱导公式、余弦定理、正弦定理、两点间距离公式等知识,考查化归与转化的数学思想方法,以及运算求解能力,属于中档题.
∵f(x)的最小正周期为8,∴
 ,得
,得 .…(2分)
.…(2分)∴f(x)=2sin(
 x+
x+ ).…(3分)
).…(3分)(2)解法1:∵
 ,…(4分)
,…(4分)∴
 ,…(5分)
,…(5分)∴
 .
.∴
 .…(8分)
.…(8分)∴
 .…(10分)
.…(10分)∴
 =
= .…(11分)
.…(11分)∴△POQ的面积为
 =
= .…(12分)
.…(12分)解法2:∵
 ,…(4分)
,…(4分)∴
 ,…(5分)
,…(5分)∴
 .
.∴直线OP的方程为
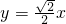 ,即
,即 .…(7分)
.…(7分)∴点Q到直线OP的距离为
 .…(9分)
.…(9分)∵
 ,…(11分)
,…(11分)∴△POQ的面积为
 =
= .…(12分)
.…(12分)分析:(1)由函数的最大值求出A,由周期求得ω,从而求得函数的解析式.
(2)解法1:先求出P、Q两点的坐标,利用两个向量的夹角公式求得cos∠POQ,可得sin∠POQ的值,根据△POQ的面积为
 ,运算求得结果.
,运算求得结果.解法2:先求出P、Q两点的坐标,利用点到直线的距离公式求得点Q到直线OP的距离d以及OP的长度,再根据△POQ的面积为
 运算求得结果.
运算求得结果.点评:本小题主要考查三角函数的图象与性质、诱导公式、余弦定理、正弦定理、两点间距离公式等知识,考查化归与转化的数学思想方法,以及运算求解能力,属于中档题.

练习册系列答案
相关题目
 (其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为
(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个点为
,且图象上一个点为 .
. 恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围. (其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为
(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个点为
,且图象上一个点为 .
. 求函数f(x)的值域;
求函数f(x)的值域; 个单位,再将图象上各点的横坐标变为原来的2倍,纵坐标不变,求经以上变换后得到的函数解析式.
个单位,再将图象上各点的横坐标变为原来的2倍,纵坐标不变,求经以上变换后得到的函数解析式. ,其中x∈R,则下列结论中正确的是( )
,其中x∈R,则下列结论中正确的是( )
 的图象左移
的图象左移 得到函数f(x)的图象
得到函数f(x)的图象 ,其中x∈R,则下列结论中正确的是( )
,其中x∈R,则下列结论中正确的是( )
 的图象左移
的图象左移 得到函数f(x)的图象
得到函数f(x)的图象 ,其中x∈R,则下列结论中正确的是( )
,其中x∈R,则下列结论中正确的是( )
 的图象左移
的图象左移 得到函数f(x)的图象
得到函数f(x)的图象