题目内容
(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分
已知梯形中,,,,、分别是、上的点,,沿将梯形翻折,使平面(如图) . 设,四面体的体积记为.
 (1) 写出表达式,并求的最大值;
(1) 写出表达式,并求的最大值;
(2) 当时,求异面直线与所成角的余弦值.
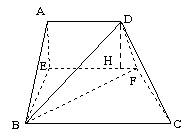
(本题14分,其中第(1)小题6分,第(2)小题8分)已知梯形ABCD中,AD∥BC,∠ABC =∠BAD =,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,设AE = 。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
(1) 若以F、B、C、D为顶点的三棱锥的体积记为,求的最大值;
(2) 当时,求异面直线AB与DF所成角的余弦值
解: (1)∵AE⊥平面EBCF
过D作DH∥AE,则DG=AE,且DH⊥平面EBCF……2分
 所以
所以
VD-BFC=
…………………………………5分
即时有最大值为。…………………………6分
(2)过A作AG∥DF,连BG,则即为异面直线AB与DF所成的角 ……………………………………9分
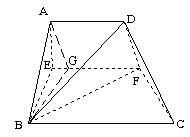 由 知EG=1 ………………………10分
由 知EG=1 ………………………10分
在⊿AEG中,……………………11分
在⊿BAEG中,……………………12分
在⊿AEBG中,…………………13分
∴………………………14分

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 ,则出厂价相应提高的比例为
,则出厂价相应提高的比例为 ,同时预计年销售量增加的比例为
,同时预计年销售量增加的比例为 .已知年利润=(出厂价–投入成本)
.已知年利润=(出厂价–投入成本) 年销售量.
年销售量. 与投入成本增加的比例
与投入成本增加的比例 的关系式;
的关系式;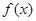 =
=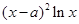 ,
,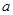 ∈R
∈R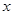 =
=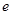 为
为 的极值点,求实数
的极值点,求实数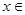 (0,3
(0,3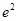 成立.
成立.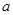 元,每期利率为
元,每期利率为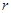 ,设存期为
,设存期为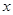 ,本利和(本金加上利息)为
,本利和(本金加上利息)为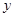 元。
元。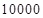 元,每期利率为
元,每期利率为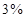 ,试计算
,试计算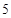 期后的本利和。
期后的本利和。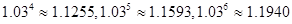 )
) 中,
中, ,
, ,
, 为
为 上的点,且
上的点,且 ,
,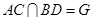 .(Ⅰ)求证:
.(Ⅰ)求证: 平面
平面 ;(Ⅱ)求证:
;(Ⅱ)求证: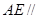 平面
平面 ;(Ⅲ)求三棱锥
;(Ⅲ)求三棱锥 的体积.
的体积.