题目内容
【题目】函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<![]() )的图象如图所示,为了得到y=cos2x的图象,则只要将f(x)的图象( )
)的图象如图所示,为了得到y=cos2x的图象,则只要将f(x)的图象( )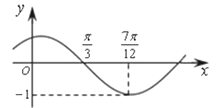
A.向左平移![]() 个单位长度
个单位长度
B.向右平移![]() 个单位长度
个单位长度
C.向左平移![]() 个单位长度
个单位长度
D.向右平移![]() 个单位长度
个单位长度
【答案】C
【解析】解:由图象可知A=1,T=π,∴ω=![]() =2
=2
∴f(x)=sin(2x+φ),又因为f(![]() )=sin(
)=sin(![]() +φ)=﹣1
+φ)=﹣1
∴![]() (k∈Z)
(k∈Z)
∵![]()
∴f(x)=sin(2x+![]() )=sin(
)=sin(![]() ﹣2x﹣
﹣2x﹣![]() )=cos(
)=cos(![]() ﹣2x)=cos(2x﹣
﹣2x)=cos(2x﹣![]() )
)
∴将函数f(x)向左平移![]() 可得到cos[2(x+
可得到cos[2(x+![]() )﹣
)﹣![]() ]=cos2x=y
]=cos2x=y
故选C.
先根据图象确定A和T的值,进而根据三角函数最小正周期的求法求ω的值,再将特殊点代入求出φ值从而可确定函数f(x)的解析式,然后根据诱导公式将函数化为余弦函数,再平移即可.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
