题目内容
直线y=2x+b是曲线y=lnx(x>0)的一条切线,则实数b=
- A.2-2e2
- B.ln2-4
- C.-ln2-1
- D.ln2-1
C
分析:求出曲线的导数,利用导数为2,求出切点坐标,然后求出b的值.
解答:曲线y=lnx(x>0)的导数为:y ,
,
由题意直线y=2x+b是曲线y=lnx(x>0)的一条切线,可知 ,
,
所以x= ,所以切点坐标为(
,所以切点坐标为( ,-ln2),
,-ln2),
切点在直线上,所以
b=y-2x=-ln2-1.
故选C.
点评:本题是基础题,考查曲线的导数与切线方程的关系,考查计算能力.
分析:求出曲线的导数,利用导数为2,求出切点坐标,然后求出b的值.
解答:曲线y=lnx(x>0)的导数为:y
 ,
,由题意直线y=2x+b是曲线y=lnx(x>0)的一条切线,可知
 ,
,所以x=
 ,所以切点坐标为(
,所以切点坐标为( ,-ln2),
,-ln2),切点在直线上,所以
b=y-2x=-ln2-1.
故选C.
点评:本题是基础题,考查曲线的导数与切线方程的关系,考查计算能力.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
已知曲线C: ,直线l:y=2x+b,那么曲C与直线l相切的充要条件是
,直线l:y=2x+b,那么曲C与直线l相切的充要条件是
A.b= | B.b=- | C.b=5 | D.b= 或b=- 或b=- |
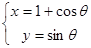 ,直线l:y=2x+b,那么曲C与直线l相切的充要条件是
,直线l:y=2x+b,那么曲C与直线l相切的充要条件是 B.b=-
B.b=- ;④y=2x+1。
;④y=2x+1。