题目内容
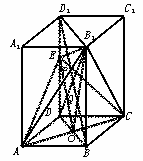
已知：在正四棱柱A1B1C1D1-ABCD中，棱AB=2，棱BB1=4，点M是棱DD1中点
（I）求三棱锥C1-ACM的体积V；
（Ⅱ）求点C1到平面ACM的距离．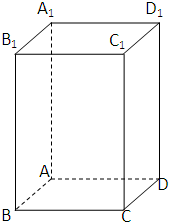
（I）求三棱锥C1-ACM的体积V；
（Ⅱ）求点C1到平面ACM的距离．
（I）由题意，VC1-ACM=VA-C1CM=
S△CMC1•AD=
•
•4•2•2=
；
（II）设点C1到平面ACM的距离为h，则
△ACM中，AC=MA=MC=2
，∴S△ACM=
•(2
)2=2
∴
=
•2
h
∴h=
．
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |
（II）设点C1到平面ACM的距离为h，则
△ACM中，AC=MA=MC=2
| 2 |
| ||
| 4 |
| 2 |
| 3 |
∴
| 8 |
| 3 |
| 1 |
| 3 |
| 3 |
∴h=
4
| ||
| 3 |
练习册系列答案
相关题目
如图，已知正四棱柱ABCD-A1B1C1D1，点E在棱D1D上，截面EAC∥D1B，且面EAC与底面ABCD所成的角为45°，AB=a．
