Question

从5名男生和4名女生中选出4人去参加辩论比赛．
（1）求参加辩论比赛的4人中有2名女生的概率；
（2）设ξ为参加辩论比赛的女生人数，求ξ的分布列及数学期望．

Answer 1

解：（1）参加辩论比赛的4人中有2名女生的概率为（ 3分）=（5分）
（2）ξ=0，1，2，3，4（6分），则
（ 7分）； （8分）
（9分）；（10分）
所求的分布列为：

ξ	0	1	2	3	4
P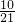

（11分）
∴（13分）=（14分）
分析：（1）参加辩论比赛的4人中有2名女生，是指2名男生，2名女生，故可求其概率；
（2）ξ=0，1，2，3，4，求出相应的概率，即可求得ξ的分布列及数学期望．
点评：本题考查概率的求解，考查离散型随机变量的分布列与期望，解题的关键是正确理解事件，求概率，确定变量的取值，属于中档题．