题目内容
已知点M(-2,0),N(2,0),动点P满足条件![]() .记动点
.记动点![]() 的轨迹为W.
的轨迹为W.
(Ⅰ)求W的方程;
(Ⅱ)若A,B是W上的不同两点,O是坐标原点,求![]() 的最小值.
的最小值.
解:(Ⅰ)依题意,点P的轨迹是以M,N为焦点的双曲线的右支,
所求方程为:![]() (x>0)
(x>0)
(Ⅱ)当直线AB的斜率不存在时,设直线AB的方程为x=x0,
此时A(x0,![]() ),B(x0,-
),B(x0,-![]() ),
),![]() =2
=2
当直线AB的斜率存在时,设直线AB的方程为y=kx+b,
代入双曲线方程![]() 中,得:(1-k2)x2-2kbx-b2-2=0
中,得:(1-k2)x2-2kbx-b2-2=0
依题意可知方程1°有两个不相等的正数根,设A(x1,y1),B(x2,y2),则
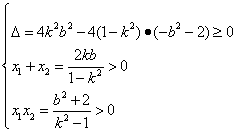 解得|k|>1,
解得|k|>1,
又![]() =x1x2+y1y2=x1x2+(kx1+b)(kx2+b)
=x1x2+y1y2=x1x2+(kx1+b)(kx2+b)
=(1+k2)x1x2+kb(x1+x2)+b2=![]() >2
>2
综上可知![]() 的最小值为2
的最小值为2

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
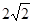 ,记动点P的轨迹为C.
,记动点P的轨迹为C.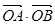 的最小值.
的最小值.