题目内容
已知函数
,
（其中
且
）.
（1）讨论函数
的单调性；
（2）若
，求函数
,
的最值；
（3）设函数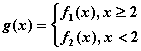
,当
时，若对于任意的
，总存在唯一
的
，使得
成立．试求
的取值范围．
答案
（2）由
，可得
。
（4分）。由（1）知，当时，
在
上是减函数。而
在上也是减函数，
当
时，
取最大值
（5分）；当
时，取最小值
。（6分）
（3）当
时，
。由（1）知，此时函数
在
上是减函数，从而
，即
（8分）。
当，由于
，则
，
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
，（其中
且
）。
的定义域；
时，函数
，求实数
的值。
，
，其中
且
．
，求函数
的单调递增区间；
时，函数
有极值，求函数
（
是自然对数的底数），是否存在a使
在
上为减函数，若存在，求实数a的范围；若不存在，请说明理由．
，
，其中
且
．
，求函数
的单调递增区间；
时，函数
有极值，求函数
（
是自然对数的底数），是否存在a使
在
上为减函数，若存在，求实数a的范围；若不存在，请说明理由．
满足
，其中
且
．
时，
，求实数
的取值集合；
时，
恒成立，求
的取值范围．
，（其中
且
）。
的定义域；
时，函数
，求实数
的值。