题目内容
已知实数a,b,c,d成等差数列,且曲线y=ln(x+2)-x的极大值点坐标为(b,c),则a+d等于
- A.-1
- B.0
- C.1
- D.2
B
分析:先求曲线y=ln(x+2)-x的导函数,令导函数为0求的b.再把点(b,c)代入曲线方程求得b+c的值,最后根据等差数列的性质可知a+d=b+c,答案可得.
解答:∵y=ln(x+2)-x
∴y•=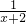 -1
-1
∵极大值点坐标为(b,c),
∴ -1=0,解得b+2=1
-1=0,解得b+2=1
∵曲线y=ln(x+2)-x的极大值点坐标为(b,c),
∴ln(b+2)-b=c,即b+c=ln(b+2)=0
∵a,b,c,d成等差数列,
∴a+d=b+c=0
故选B
点评:本题主要考查了等差数列的性质和用导函数研究函数极值的问题.考查了学生综合分析问题的能力.
分析:先求曲线y=ln(x+2)-x的导函数,令导函数为0求的b.再把点(b,c)代入曲线方程求得b+c的值,最后根据等差数列的性质可知a+d=b+c,答案可得.
解答:∵y=ln(x+2)-x
∴y•=
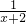 -1
-1∵极大值点坐标为(b,c),
∴
 -1=0,解得b+2=1
-1=0,解得b+2=1∵曲线y=ln(x+2)-x的极大值点坐标为(b,c),
∴ln(b+2)-b=c,即b+c=ln(b+2)=0
∵a,b,c,d成等差数列,
∴a+d=b+c=0
故选B
点评:本题主要考查了等差数列的性质和用导函数研究函数极值的问题.考查了学生综合分析问题的能力.

练习册系列答案
相关题目