题目内容
设抛物线y2=2px(p>0)的焦点为F,过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC∥x轴,求证:AC过原点O.
分析:证明直线AC经过点O,只需证明![]() ∥
∥![]() 即可.
即可.
证明:设直线AB的方程为x=ky+![]() ,与抛物线联立得y2-2pky-p2=0. ①
,与抛物线联立得y2-2pky-p2=0. ①
设A(![]() ,y1)、B(
,y1)、B(![]() ,y2),则C(-
,y2),则C(-![]() ,y2),
,y2), ![]() =(-
=(-![]() ,y2)
,y2) ![]() =(
=(![]() ,y1).
,y1).
由①得y1y2=-p2,所以-![]() y1-y2·
y1-y2·![]() =0
=0![]()
![]() ∥
∥![]() .所以AC经过原点O.
.所以AC经过原点O.
说明:本题的解法很多,下面用向量a、b共线的充要条件a=λb来证明.
由AB过焦点F,得![]() +
+![]() =
=![]() ,
,
所以![]() =
=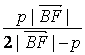 ,
,![]() =
=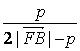
![]() . (*)
. (*)
因为点C在抛物线的准线上,BC∥x轴,所以
|![]() |=|
|=|![]() |,
|,![]() =
=![]() +
+![]() +
+![]() =
=![]() +
+![]() +
+![]()
![]() =
= ![]() +
+![]() +
+![]()
![]() ,
,![]() =
=![]() +
+![]() .将
.将![]() 、
、![]() 代入(*)式得
代入(*)式得![]() +
+![]() =
=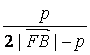 (
(![]() +
+![]() +
+![]()
![]() ),化简得
),化简得![]() =
=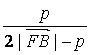
![]() ,所以
,所以![]() ∥
∥![]() ,即直线AC过原点O.
,即直线AC过原点O.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
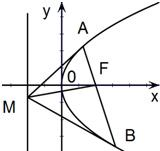 设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,且A,B两点坐标分别为(x1,y1)、(x2,y2),y1>0,y2<0,M是抛物线的准线上的一点,O是坐标原点.若直线MA,MF,MB的斜率分别记为:KMA=a,KMF=b,KMB=c,(如图)
设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,且A,B两点坐标分别为(x1,y1)、(x2,y2),y1>0,y2<0,M是抛物线的准线上的一点,O是坐标原点.若直线MA,MF,MB的斜率分别记为:KMA=a,KMF=b,KMB=c,(如图)