题目内容
已知 分别是
分别是 的三个内角
的三个内角 的对边,
的对边, .
.
(1)求角 的大小;
的大小;
(2)求函数 的值域.
的值域.
 分别是
分别是 的三个内角
的三个内角 的对边,
的对边, .
.(1)求角
 的大小;
的大小;(2)求函数
 的值域.
的值域.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)若在三角形中求角,一般情况可把等式里的边由正弦定理化为角,再化简,可得角
 的大小;(2)由(1)知在三角形中角
的大小;(2)由(1)知在三角形中角 的大小,则可知
的大小,则可知 的大小,即知角
的大小,即知角 的范围,再化简所求函数,根据角
的范围,再化简所求函数,根据角 的范围求函数的值域.
的范围求函数的值域.试题解析:(I)由正弦定理,得:
 , 2分
, 2分即
 ,
,故
 , 4分
, 4分 , 所以
, 所以 . 6分
. 6分(II)
 , 8分
, 8分 11分
11分 , 13分
, 13分所以所求函数值域为
 . 14分
. 14分
练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
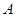 、
、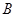 、
、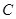 三个工作点,需要建立一个公共无线网络发射点
三个工作点,需要建立一个公共无线网络发射点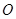 ,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为
,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为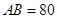
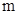 ,
,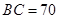
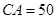
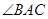 的大小;
的大小;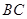 的距
的距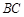 ,已知石塔的高度为
,已知石塔的高度为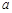 .
.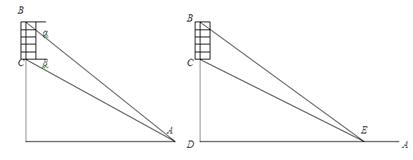
 为观测点,在塔顶
为观测点,在塔顶 处测得地面上一点
处测得地面上一点 的俯角为
的俯角为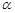 ,在塔底
,在塔底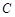 处测得
处测得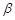 ,用
,用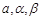 表示山的高度
表示山的高度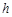 ;
;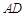 上,其中
上,其中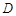 是塔顶
是塔顶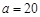 ,当观测点
,当观测点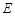 在
在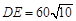 时看
时看 )最大,求山的高度
)最大,求山的高度 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, ,
, .
. 的值;
的值; 的值.
的值.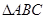 中,角
中,角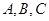 所对的边分别为
所对的边分别为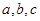 ,且满足
,且满足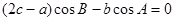
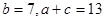 ,求
,求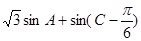 的取值范围.
的取值范围.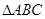 ,
,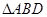 ,经测量
,经测量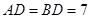 米,
米,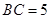 米,
米,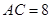 米,
米, .
.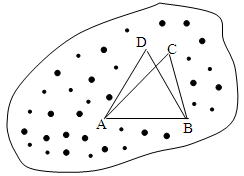
 的长度;
的长度;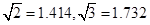 )
) 中,内角
中,内角 所对边长分别为
所对边长分别为 ,若
,若 ,则
,则



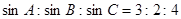 ,则cosC的值为 ( )
,则cosC的值为 ( )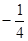
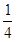
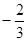
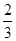
 中,
中, ,则
,则
