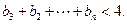题目内容
(本小题14分)已知数列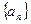 为等差数列,
为等差数列,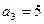 ,
,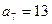 ,数列
,数列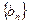 的前
的前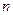 项和为
项和为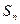 ,且有
,且有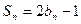
(1)求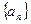 、
、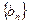 的通项公式;
的通项公式;
(2)若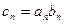 ,
,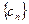 的前
的前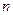 项和为
项和为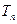 ,求
,求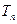 ;
;
(3)试比较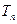 与
与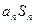 的大小,并说明理由.
的大小,并说明理由.
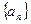 为等差数列,
为等差数列,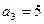 ,
,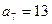 ,数列
,数列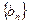 的前
的前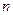 项和为
项和为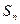 ,且有
,且有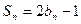
(1)求
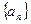 、
、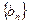 的通项公式;
的通项公式;(2)若
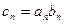 ,
,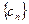 的前
的前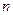 项和为
项和为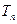 ,求
,求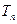 ;
;(3)试比较
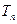 与
与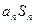 的大小,并说明理由.
的大小,并说明理由.解:(1)∵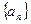 是等差数列,且
是等差数列,且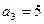 ,
,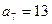 ,设公差为
,设公差为 。
。
∴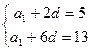 , 解得
, 解得
∴ (
( ) …2分
) …2分
在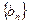 中,∵
中,∵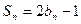
当 时,
时, ,∴
,∴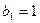
当 时,由
时,由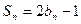 及
及 可得
可得
 ,∴
,∴
∴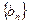 是首项为1公比为2的等比数列
是首项为1公比为2的等比数列
∴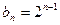 (
( ) …4分
) …4分
(2)
 ①
①
 ②
②
①-②得
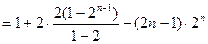

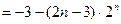
∴ (
( ) …8分
) …8分
(3)

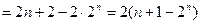 …9分
…9分
令 ,则
,则
∵ 在
在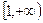 是减函数,又
是减函数,又
∴ 时,
时,
∴ 时,
时,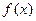 是减函数.
是减函数.
又
∴ 时,
时,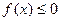
∴ 时,
时,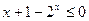 …13分
…13分
∴ 时,
时,
∴ 时,
时, …14分
…14分
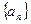 是等差数列,且
是等差数列,且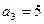 ,
,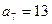 ,设公差为
,设公差为 。
。∴
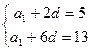 , 解得
, 解得
∴
 (
( ) …2分
) …2分在
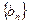 中,∵
中,∵
当
 时,
时, ,∴
,∴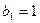
当
 时,由
时,由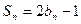 及
及 可得
可得 ,∴
,∴
∴
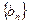 是首项为1公比为2的等比数列
是首项为1公比为2的等比数列∴
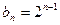 (
( ) …4分
) …4分(2)

 ①
① ②
②①-②得

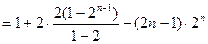

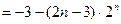
∴
 (
( ) …8分
) …8分(3)


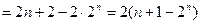 …9分
…9分令
 ,则
,则
∵
 在
在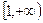 是减函数,又
是减函数,又
∴
 时,
时,
∴
 时,
时,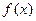 是减函数.
是减函数.又

∴
 时,
时,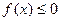
∴
 时,
时,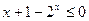 …13分
…13分∴
 时,
时,
∴
 时,
时, …14分
…14分略

练习册系列答案
相关题目
 是等差数列,
是等差数列,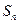 为其前n项和,若
为其前n项和,若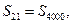 O为坐标原点,点P(1,
O为坐标原点,点P(1,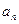 ),点Q(2011,
),点Q(2011,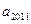 ),则
),则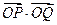 ( )
( )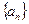 的前四项分别为1,0,1,0,则下列各式可以作为数列
的前四项分别为1,0,1,0,则下列各式可以作为数列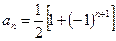 ②
②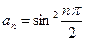
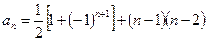
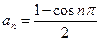 ⑤
⑤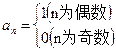
 的三边
的三边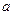 、
、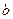 、
、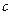 成等差且均为整数,公差为
成等差且均为整数,公差为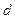 ,则下列命题不正确的是( )
,则下列命题不正确的是( )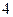 的倍数
的倍数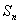 是数列{
是数列{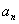 }的前n项和,并且
}的前n项和,并且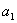 =1,对任意正整数n,
=1,对任意正整数n,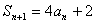 ;设
;设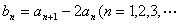 ).(I)证明数列
).(I)证明数列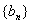 是等比数列,并求
是等比数列,并求 的前n项和,求
的前n项和,求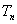 .
.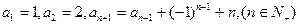
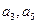 的值;
的值;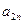 ;
;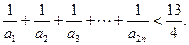
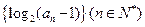 为等差数列,且
为等差数列,且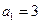 ,
,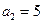 ,则
,则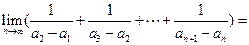 ___
___ _________.
_________.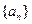 中,
中,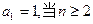 时,其前
时,其前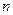 项和
项和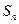 满足:
满足: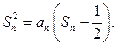
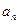 ;
;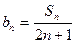 ,求数列
,求数列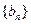 的前项和
的前项和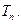
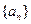 的前n项和为
的前n项和为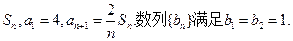
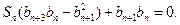
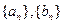 的通项公式;
的通项公式;