题目内容
设数列{an}的前n项和为Sn,对任意的正整数n,都有an=5Sn+1成立,记bn=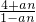 (n∈N*)
(n∈N*)
(1)求数列{an}与数列{bn}的通项公式;
(2)记cn=b2n-b2n-1 (n∈N*),设数列{cn}的前n项和为Tn,求证:对任意正整数n都有Tn< ;
;
(3)设数列{bn}的前n项和为Rn,是否存在正整数k,使得Rk≥4k成立?若存在,找出一个正整数k;若不存在,请说明理由.
解:(1)当n=1时,a1=5S1+1,∴a1=- (1分)
(1分)
又∵an=5Sn+1,an+1=5Sn+1+1,∴an+1-an=5an+1即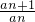 =-
=-
∴数列{an}是首项为a1=- ,公比为q=-
,公比为q=- 的等比数列,(3分)
的等比数列,(3分)
∴an=(- )n,bn=
)n,bn=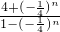 (n∈N* )(5分)
(n∈N* )(5分)
(2)由(1)知bn=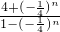 =4+
=4+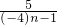 得
得
cn=b2n-b2n-1=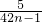 +
+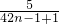 =
=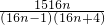 =
= <
<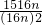 =
=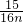 (7分)
(7分)
又b1=3,b2= ,∴c1=
,∴c1= ,所以当n=1时,T1<
,所以当n=1时,T1< ,(8分)
,(8分)
当n≥2时,Tn< +15(
+15(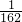 +
+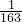 ++
++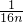 )=
)= +15•
+15•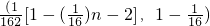 <
< +
+ =
=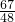 <
< (10分)
(10分)
(3)不存在正整数k,使得RK≥4K成立.(11分)
证明:由bn=4+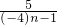
∵b2k-1+b2k=8+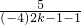 +
+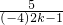 =8+
=8+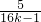 -
-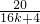 =8-
=8-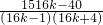 <8(13分)
<8(13分)
∴当n为偶数时,设n=2m(m∈N*)
∴Rn=(b1+b2)+(b3+b4)+…+(b2m-1+b2m)<8m=4n(14分)
当n为奇数时,设n=2m-1(m∈N*)
∴Rn=(b1+b2)+(b3+b4)+…+(b2m-3+b2m-2)+b2m-1<8m-4=4n
∴Rn=(b1+b2)+(b3+b4)+…+(b2m-3+b2m-2)+b2m-1<8(m-1)+4=8m-4=4n(15分)
∴对于一切的正整数n,都有Rn<4n
∴不存在正整数k,使得RK≥4K成立.(16分)
分析:(1)令n等于1代入an=5Sn+1中,即可求出首项a1,然后把n换为n+1,利用an=5Sn+1表示出an+1,两个式子相减并利用Sn+1-Sn=an化简后即可得到 的值即为公比,得到此数列为等比数列,然后根据首项和公比写出数列的通项公式即可,因而可得出bn的通项公式;
的值即为公比,得到此数列为等比数列,然后根据首项和公比写出数列的通项公式即可,因而可得出bn的通项公式;
(2)根据bn的通项公式,计算出cn的通项公式,再比较Tn与 的大小;
的大小;
(3)根据bn的通项公式,算出的前n项和为Rn,再计算出是否存在正整数k.
点评:此题考查学生灵活运用等比数列的通项公式及前n项和的公式化简求出,会确定一个数列为等比数列,考查数列递推式的求解及相关计算.是一道综合题.
 (1分)
(1分)又∵an=5Sn+1,an+1=5Sn+1+1,∴an+1-an=5an+1即
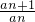 =-
=-
∴数列{an}是首项为a1=-
 ,公比为q=-
,公比为q=- 的等比数列,(3分)
的等比数列,(3分)∴an=(-
 )n,bn=
)n,bn=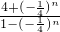 (n∈N* )(5分)
(n∈N* )(5分)(2)由(1)知bn=
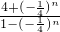 =4+
=4+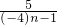 得
得cn=b2n-b2n-1=
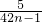 +
+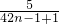 =
=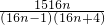 =
= <
<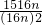 =
=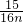 (7分)
(7分)又b1=3,b2=
 ,∴c1=
,∴c1= ,所以当n=1时,T1<
,所以当n=1时,T1< ,(8分)
,(8分)当n≥2时,Tn<
 +15(
+15(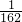 +
+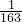 ++
++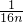 )=
)= +15•
+15•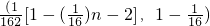 <
< +
+ =
=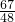 <
< (10分)
(10分)(3)不存在正整数k,使得RK≥4K成立.(11分)
证明:由bn=4+
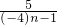
∵b2k-1+b2k=8+
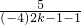 +
+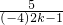 =8+
=8+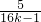 -
-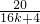 =8-
=8-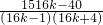 <8(13分)
<8(13分)∴当n为偶数时,设n=2m(m∈N*)
∴Rn=(b1+b2)+(b3+b4)+…+(b2m-1+b2m)<8m=4n(14分)
当n为奇数时,设n=2m-1(m∈N*)
∴Rn=(b1+b2)+(b3+b4)+…+(b2m-3+b2m-2)+b2m-1<8m-4=4n
∴Rn=(b1+b2)+(b3+b4)+…+(b2m-3+b2m-2)+b2m-1<8(m-1)+4=8m-4=4n(15分)
∴对于一切的正整数n,都有Rn<4n
∴不存在正整数k,使得RK≥4K成立.(16分)
分析:(1)令n等于1代入an=5Sn+1中,即可求出首项a1,然后把n换为n+1,利用an=5Sn+1表示出an+1,两个式子相减并利用Sn+1-Sn=an化简后即可得到
 的值即为公比,得到此数列为等比数列,然后根据首项和公比写出数列的通项公式即可,因而可得出bn的通项公式;
的值即为公比,得到此数列为等比数列,然后根据首项和公比写出数列的通项公式即可,因而可得出bn的通项公式;(2)根据bn的通项公式,计算出cn的通项公式,再比较Tn与
 的大小;
的大小;(3)根据bn的通项公式,算出的前n项和为Rn,再计算出是否存在正整数k.
点评:此题考查学生灵活运用等比数列的通项公式及前n项和的公式化简求出,会确定一个数列为等比数列,考查数列递推式的求解及相关计算.是一道综合题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目