题目内容
若向量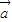 =(cosα,sinα),
=(cosα,sinα),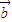 =(cosβ,sinβ),且α-β=kπ(k∈Z),则
=(cosβ,sinβ),且α-β=kπ(k∈Z),则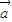 与
与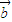 一定满足:①
一定满足:①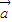 与
与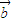 夹角等于α-β;②|
夹角等于α-β;②|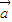 |=|
|=|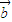 |;③
|;③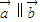 ;④
;④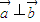 .其中正确结论的序号为 .
.其中正确结论的序号为 .
【答案】分析:利用向量夹角有范围,判断出①错;利用向量模的坐标公式求出两个向量的模,判断出②对;利用α,β的关系,将
的坐标用β表示,利用向量共线的充要条件判断出③对,从而得到④错.
解答:解:由于向量夹角的范围是[0,π],显然①不对.
对于②:| |=
|= =1,
=1,
| |=
|= =1.
=1.
∴| |=|
|=| |,故②正确.
|,故②正确.
对于③:∵cosα=cos(kπ+β)= ,
,
sinα=sin(kπ+β)= ,
,
∴ =(cosβ,sinβ)或
=(cosβ,sinβ)或 =(-cosβ,-sinβ),与
=(-cosβ,-sinβ),与 平行.故③正确.
平行.故③正确.
由③得到显然④不正确.
故答案为:②③
点评:本题考查向量模的坐标公式、考查向量共线的充要条件、考查向量垂直的充要条件.

的坐标用β表示,利用向量共线的充要条件判断出③对,从而得到④错.
解答:解:由于向量夹角的范围是[0,π],显然①不对.
对于②:|
 |=
|= =1,
=1,|
 |=
|= =1.
=1.∴|
 |=|
|=| |,故②正确.
|,故②正确.对于③:∵cosα=cos(kπ+β)=
 ,
,sinα=sin(kπ+β)=
 ,
,∴
 =(cosβ,sinβ)或
=(cosβ,sinβ)或 =(-cosβ,-sinβ),与
=(-cosβ,-sinβ),与 平行.故③正确.
平行.故③正确.由③得到显然④不正确.
故答案为:②③
点评:本题考查向量模的坐标公式、考查向量共线的充要条件、考查向量垂直的充要条件.

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
若向量
=(cosα,sinα),
=(cosβ,sinβ),则
与
一定满足( )
| a |
| b |
| a |
| b |
A、
| ||||||||
B、(
| ||||||||
C、
| ||||||||
D、
|
若向量
=(cosα,sinβ),
=(cosα,sinβ),则
与
一定满足( )
| a |
| b |
| a |
| b |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、(
|