题目内容
14．在7名运动员中选4名运动员组成接力队，参加4×100m接力赛，那么甲乙两人都不跑中间两棒的安排方法有多少种？分析 第一步，安排中间2个位置，第二步，安排首尾2个位置，利用乘法原理可得结论．
解答 解：第一步中间位置除了甲乙还有5人，5个选2个全排列跑中间两棒，有${A}_{5}^{2}$=20种；
第二步确定首尾的人选，还剩下5个人，选2个全排列，有${A}_{5}^{2}$=20种．
两步相乘，共有20×20=400种．
点评 本题考查计数原理的运用问题，解题的关键是正确分步．注意甲乙都不跑中间，包括了甲乙可能都不上场的情形．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
5．对于定义在实数集R上的函数f（x），如果存在实数x0，使f（x0）=x0，那么x0叫做函数f（x）的一个好点．已知函数f（x）=x2+2ax+1不存在好点，那么a的取值范围是（ ）
| A． | （-$\frac{1}{2}$，$\frac{3}{2}$） | B． | （-$\frac{3}{2}$，$\frac{1}{2}$） | C． | （-1，1） | D． | （-∞，1）∪（1，+∞） |
2．已知椭圆$\frac{{x}^{2}}{4}+{y}^{2}=1$的焦点为F1，F2，在长轴A1A2上任取一点M，过M作垂直于A1A2的直线交椭圆于点P，则∠F1PF2为钝角的概率为（ ）
| A． | $\frac{\sqrt{2}}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{{2\sqrt{2}}}{3}$ | D． | $\frac{\sqrt{6}}{3}$ |
9．已知正方体ABCD-A1B1C1D1的棱长为l，动点P在正方体表面上且满足|PA|=|PC1|，则动点P的轨迹长度为（ ）
| A． | 3 | B． | 3$\sqrt{2}$ | C． | 3$\sqrt{3}$ | D． | 6 |
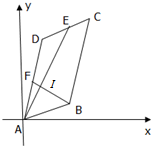如图，已知平行四边形ABCD的顶点A（0，0），B（4，1），C（6，8）