题目内容
已知一个样本的方差s2=
[(x1-3)2+(x2-3)2+…+(xn-3)2],则这组数据的总和等于
| 1 | 20 |
60
60
.分析:根据样本的方差的知这组数据的容量和平均数,从而求出这组数据的总和.
解答:解:由于这组数据的样本的方差是:s2=
[(x1-3)2+(x2-3)2+…+(xn-3)2],
根据方差的计算公式可知,
这组数据的样本容量为n=20,平均数为
=3,
则这组数据等总和等于S=n×
=20×3=60,
故答案为:60.
| 1 |
| 20 |
根据方差的计算公式可知,
这组数据的样本容量为n=20,平均数为
. |
| x |
则这组数据等总和等于S=n×
. |
| x |
故答案为:60.
点评:本题考查平均数和方差,本题解题的关键是理解这几个特征数的特点与求法,本题是一个基础题.

练习册系列答案
相关题目
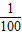 [(x1-24)2+(x2-24)2+…+(x100-24)2],若这个样本的容量为n,平均数为μ,则n-2μ=( )
[(x1-24)2+(x2-24)2+…+(x100-24)2],若这个样本的容量为n,平均数为μ,则n-2μ=( )