题目内容
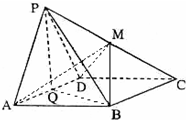 (2013•牡丹江一模)如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
(2013•牡丹江一模)如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.(1)求证:AD⊥平面PQB;
(2)若平面PAD⊥平面ABCD,且PM=
| 1 | 2 |
分析:(1)连接BD,等边三角形PAD中,中线PQ⊥AD;因为菱形ABCD中∠BAD=60°,所以AD⊥BQ,最后由线面垂直的判定定理即可证出AD⊥平面PQB;
(2)连接QC,作MH⊥QC于H.因为平面PAD⊥平面ABCD,PQ⊥AD,结合面面垂直性质定理证出PQ⊥平面ABCD.而平面PQC中,PQ∥MH,可得MH⊥平面ABCD,即MH就是四棱锥M-ABCD的高线.最后利用锥体体积公式结合题中数据即可算出四棱锥M-ABCD的体积.
(2)连接QC,作MH⊥QC于H.因为平面PAD⊥平面ABCD,PQ⊥AD,结合面面垂直性质定理证出PQ⊥平面ABCD.而平面PQC中,PQ∥MH,可得MH⊥平面ABCD,即MH就是四棱锥M-ABCD的高线.最后利用锥体体积公式结合题中数据即可算出四棱锥M-ABCD的体积.
解答:解:(1)连接BD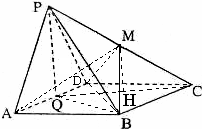
∵PA=PD=AD=2,Q为AD的中点,
∴PQ⊥AD
又∵∠BAD=60°,底面ABCD为菱形,
∴△ABD是等边三角形,
∵Q为AD的中点,∴AD⊥BQ
∵PQ、BQ是平面PQB内的相交直线,∴AD⊥平面PQB.
(2)连接QC,作MH⊥QC于H.
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PQ⊥AD
∴PQ⊥平面ABCD,结合QC?平面ABCD,可得PQ⊥QC
∵平面PQC中,MH⊥QC且PQ⊥QC,
∴PQ∥MH,可得MH⊥平面ABCD,即MH就是四棱锥M-ABCD的高线
∵PM=
PC,可得MH=
PQ=
×
×2=
,
∴四棱锥M-ABCD的体积为VM-ABCD=
×
AC×BD×MH=
×2×2
×
=1.

∵PA=PD=AD=2,Q为AD的中点,
∴PQ⊥AD
又∵∠BAD=60°,底面ABCD为菱形,
∴△ABD是等边三角形,
∵Q为AD的中点,∴AD⊥BQ
∵PQ、BQ是平面PQB内的相交直线,∴AD⊥平面PQB.
(2)连接QC,作MH⊥QC于H.
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PQ⊥AD
∴PQ⊥平面ABCD,结合QC?平面ABCD,可得PQ⊥QC
∵平面PQC中,MH⊥QC且PQ⊥QC,
∴PQ∥MH,可得MH⊥平面ABCD,即MH就是四棱锥M-ABCD的高线
∵PM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴四棱锥M-ABCD的体积为VM-ABCD=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 3 |
| ||
| 2 |
点评:本题给出特殊四棱锥,求证线面垂直并求锥体体积,着重考查了直线与平面垂直的判定、平面与平面垂直的性质和体积公式等知识,属于中档题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 (2013•牡丹江一模)已知四棱锥P-ABCD的三视图如图所示,则四棱锥P-ABCD的四个侧面中面积最大的是( )
(2013•牡丹江一模)已知四棱锥P-ABCD的三视图如图所示,则四棱锥P-ABCD的四个侧面中面积最大的是( )