Question

如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA  ⊥平面ABCD,AP=AB=2,BC=2 √  2，E，F分别

AD，PC的重点    

 

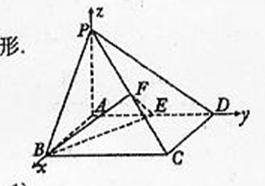
（Ⅰ）证明：PC  ⊥平面BEF；

（Ⅱ）求平面BEF与平面BAP夹角的大小。

Answer 1

解法一  （Ⅰ）如图，以A为坐标原点，AB，AD，AP算在直线分别为x，y，z轴建立空间直角坐标系。

∵AP=AB=2,BC=AD=2√  2,四边形ABCD是矩形。

∴A，B，C，D的坐标为A(0,0,0),B(2,0,0),C(2, 2 √  2,0)，D(0，2 √  2，0)，P(0,0,2)

又E，F分别是AD，PC的中点，

∴E(0，√  2，0),F(1，√  2，1)。

∴=（2，2 √  2，-2）=（-1，√  2，1）=（1,0,1），

∴·=-2+4-2=0，·=2+0-2=0，

∴⊥，⊥，

∴PC⊥BF,PC⊥EF,BF ∩  EF=F,[来源:Zxxk.Com]

∴PC⊥平面BEF

（II）由（I）知平面BEF的法向量

平面BAP 的法向量

  设平面BEF与平面BAP的夹角为 θ ，

则

∴ θ=45℃， ∴ 平面BEF与平面BAP的夹角为45

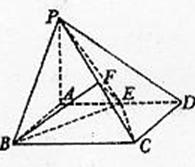
解法二  （I）连接PE，EC在

PA=AB=CD, AE=DE,

∴ PE= CE, 即 △PEC 是等腰三角形，

又F是PC 的中点，∴EF⊥PC,

又，F是PC 的中点，

∴BF⊥PC.[来源:学§科§网Z§X§X§K]

又