题目内容
已知函数f(x)=2cos2x+cos(2x+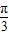 )
)(1)在锐角△ABC中,a,b,c分别是角A,B,C的对边;若
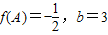 ,sin(A+C)=
,sin(A+C)= sinC,求△ABC的面积.
sinC,求△ABC的面积.(2)若f(α)=
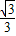 +1,0<α<
+1,0<α<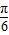 ,求sin2α的值.
,求sin2α的值.
【答案】分析:(1)利用二倍角、辅助角公式,化简函数,结合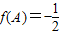 ,可求A,再结合正弦定理,可求c,从而可求△ABC的面积.
,可求A,再结合正弦定理,可求c,从而可求△ABC的面积.
(2)由f(α)=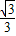 +1,0<α<
+1,0<α<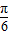 ,可求sin(2α+
,可求sin(2α+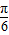 )=
)=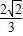 ,从而可求sin2α的值.
,从而可求sin2α的值.
解答:解:(1)函数f(x)=2cos2x+cos(2x+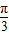 )=1+cos2x+
)=1+cos2x+ cos2x-
cos2x-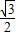 sin2x=1+
sin2x=1+ cos2x-
cos2x-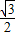 sin2x=
sin2x=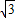 cos(2x+
cos(2x+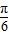 )+1
)+1
∵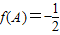 ,∴
,∴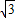 cos(2A+
cos(2A+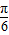 )+1=-
)+1=- ,∴cos(2A+
,∴cos(2A+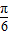 )=-
)=-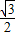 .
.
∵A∈(0,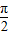 ),∴2A+
),∴2A+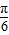 ∈(
∈(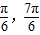 ),∴2A+
),∴2A+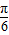 =
=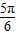 ,即A=
,即A=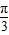 .
.
又因为sin(A+C)= sinC,即sinB=
sinC,即sinB= sinC,由正弦定理得
sinC,由正弦定理得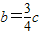 ,
,
又b=3,∴c=4.
∴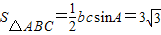
(2)f(α)=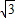 cos(2α+
cos(2α+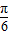 )+1=
)+1=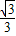 +1,则cos(2α+
+1,则cos(2α+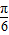 )=
)=
∵0<α<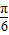 ,∴0<2α+
,∴0<2α+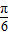 <
<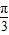 ,∴sin(2α+
,∴sin(2α+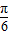 )=
)=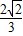
∴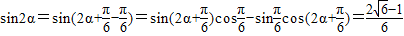
点评:本题考查三角函数的化简,考查正弦定理,考查角的变换,考查学生的计算能力,属于中档题.
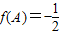 ,可求A,再结合正弦定理,可求c,从而可求△ABC的面积.
,可求A,再结合正弦定理,可求c,从而可求△ABC的面积.(2)由f(α)=
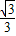 +1,0<α<
+1,0<α<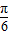 ,可求sin(2α+
,可求sin(2α+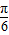 )=
)=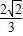 ,从而可求sin2α的值.
,从而可求sin2α的值.解答:解:(1)函数f(x)=2cos2x+cos(2x+
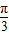 )=1+cos2x+
)=1+cos2x+ cos2x-
cos2x-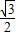 sin2x=1+
sin2x=1+ cos2x-
cos2x-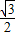 sin2x=
sin2x=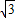 cos(2x+
cos(2x+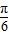 )+1
)+1∵
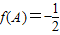 ,∴
,∴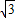 cos(2A+
cos(2A+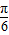 )+1=-
)+1=- ,∴cos(2A+
,∴cos(2A+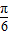 )=-
)=-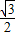 .
.∵A∈(0,
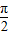 ),∴2A+
),∴2A+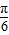 ∈(
∈(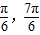 ),∴2A+
),∴2A+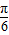 =
=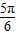 ,即A=
,即A=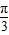 .
.又因为sin(A+C)=
 sinC,即sinB=
sinC,即sinB= sinC,由正弦定理得
sinC,由正弦定理得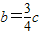 ,
,又b=3,∴c=4.
∴
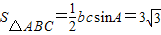
(2)f(α)=
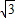 cos(2α+
cos(2α+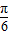 )+1=
)+1=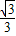 +1,则cos(2α+
+1,则cos(2α+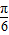 )=
)=
∵0<α<
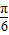 ,∴0<2α+
,∴0<2α+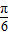 <
<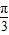 ,∴sin(2α+
,∴sin(2α+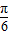 )=
)=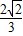
∴
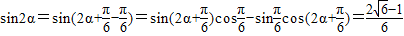
点评:本题考查三角函数的化简,考查正弦定理,考查角的变换,考查学生的计算能力,属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目