题目内容
1．设x∈R，且x≠0，若x+x-1=3，猜想${x}^{{2}^{n}}$+${x}^{-{2}^{n}}$的个位数字是7．分析 由已知中x+x-1=3，结合完全平方公式，求出n=1，2，3，…时，${x}^{{2}^{n}}$+${x}^{-{2}^{n}}$的值，分析个位数的变化规律，可得答案．
解答 解：∵x+x-1=3，
∴n=1时，x2+x-2=（x+x-1）2-2=32-2=7，
n=2时，x4+x-4=（x2+x-2）2-2=72-2=47，
n=3时，x8+x-8=（x4+x-4）2-2=472-2=2207，
…
归纳可得${x}^{{2}^{n}}$+${x}^{-{2}^{n}}$的个位数字是7，
故答案为：7
点评 归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．
练习册系列答案
口算能手系列答案
相关题目
9．
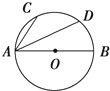如图，已知AB是圆O的直径，点C、D是半圆弧的两个三等分点，$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，则$\overrightarrow{AD}$=（ ）
如图，已知AB是圆O的直径，点C、D是半圆弧的两个三等分点，$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，则$\overrightarrow{AD}$=（ ）| A． | $\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | B． | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$ | C． | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | D． | $\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ |