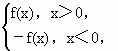题目内容
设a+b>0,n为偶数,求证:
思路分析:注意到不等式两边的幂的结构,作差后,有公因式,即可化为几个因式相乘,即而可判断等号.
证明:![]() -
-![]() -
-![]()
=![]() ,
,
当a>0,b>0时,(an-bn)(an-1-bn-1)≥0,(ab)n>0.
所以![]() ≥0.
≥0.
故![]() -
-![]() n≥
n≥![]() +
+![]() .
.
当a,b有一个为负值时,不妨设a>0,b<0,且a+b>0,所以a>|b|,又n为偶数.
所以(an-bn)(an-1-bn-1)>0.又(ab)n>0,
故![]() >0.
>0.
即![]() >
>![]() +
+![]() .
.
综上,可知原不等式成立.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 +bx+1(a、b为实数),F(x)=
+bx+1(a、b为实数),F(x)=