题目内容

已知，实数a、b、c满足f（a）f（b）f（c）＜0，且0＜a＜b＜c，若实数x是函数f（x）的一个零点，那么下列不等式中，不可能成立的是（ ）
A．x＜a
B．x＞b
C．x＜c
D．x＞c
【答案】分析：确定函数为减函数，进而可得f（a）、f（b）、f（c）中一项为负的、两项为正的；或者三项都是负的，分类讨论分别求得可能成立选项，从而得到答案．
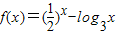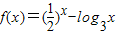解答：解：∵在（0，+∞）上是减函数，0＜a＜b＜c，且 f（a）f（b）f（c）＜0，
∴f（a）、f（b）、f（c）中一项为负的、两项为正的；或者三项都是负的．
即f（c）＜0，0＜f（b）＜f（a）；或f（a）＜f（b）＜f（c）＜0．
由于实数x是函数y=f（x）的一个零点，
当f（c）＜0，0＜f（b）＜f（a）时，b＜x＜c，此时B，C成立．
当f（a）＜f（b）＜f（c）＜0时，x＜a，此时A成立．
综上可得，D不可能成立
故选D．
点评：本题主要考查函数的零点的定义，判断函数的零点所在的区间的方法，体现了分类讨论的数学思想，属于中档题
练习册系列答案
相关题目
已知正实数a，b，c成等差数列，且a+b+c=15．
（I）求b的值；
（II）若a+1，b+1，c+4成等比数列；
（i）求a，c的值；
（ii）若a，b，c为等差数列{an}的前三项，求数列{an•xn-1}(x≠0)的前n项和．
（1）已知直线C1：
x=1+tcosα
y=tsinα
（t为参数），C2：
x=cosθ
y=sinθ
（θ为参数）．
（Ⅰ）当α=
π
3
时，求C1与C2的交点坐标；
（Ⅱ）过坐标原点O做C1的垂线，垂足为A，P为OA中点，当α变化时，求P点的轨迹的参数方程．
（2）已知正实数a、b、c满足a2+4b2+c2=3．
（I）求a+2b+c的最大值；
（II）若不等式|x-5|-|x-1|≥a+2b+c恒成立，求实数x的取值范围．
有（1）、（2）、（3）三个选考题，每题7分，请考生任选2题作答，满分14分．如果多做，则按所做的前两题记分．
（1）选修4-2：矩阵与变换
已知点A（1，0），B（2，2），C（3，0），矩阵M表示变换”顺时针旋转45°”．
（Ⅰ）写出矩阵M及其逆矩阵M-1；
（Ⅱ）请写出△ABC在矩阵M-1对应的变换作用下所得△A1B1C1的面积．
（2）选修4-4：坐标系与参数方程
过P（2，0）作倾斜角为α的直线l与曲线E：
x=cosθ
y=
2
2
sinθ
（θ为参数）交于A，B两点．
（Ⅰ）求曲线E的普通方程及l的参数方程；
（Ⅱ）求sinα的取值范围．
（3）（选修4-5 不等式证明选讲）
已知正实数a、b、c满足条件a+b+c=3，
（Ⅰ）求证：
a
+
b
+
c
≤3；
（Ⅱ）若c=ab，求c的最大值．
选考题部分
（1）（选修4-4 参数方程与极坐标）（本小题满分7分）
在极坐标系中，过曲线L：ρsin2θ=2acosθ（a＞0）外的一点A(2
5
，π+θ)（其中tanθ=2，θ为锐角）作平行于θ=
π
4
(ρ∈R)的直线l与曲线分别交于B，C．
（Ⅰ） 写出曲线L和直线l的普通方程（以极点为原点，极轴为x轴的正半轴建系）；
（Ⅱ）若|AB|，|BC|，|AC|成等比数列，求a的值．
（2）（选修4-5 不等式证明选讲）（本小题满分7分）
已知正实数a、b、c满足条件a+b+c=3，
（Ⅰ） 求证：
a
+
b
+
c
≤3；
（Ⅱ）若c=ab，求c的最大值．
已知正实数a、b、c满足条件a+b+c=3，
（Ⅰ） 求证：
a
+
b
+
c
≤3；
（Ⅱ）若c=ab，求c的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网