题目内容
设函数f（x）在定义域R内恒有f（-x）+f（x）=0，当x≤0时，
，则f（1）=________．
分析：由条件判断出函数是奇函数，由f（0）=0求出a的值，再由奇函数的定义得f（1）=-f（-1），代入所给的解析式求值．
解答：由f（-x）+f（x）=0，得f（x）=-f（x），
∴函数f（x）在定义域R内是奇函数，即f（0）=0，
∵当x≤0时，
，∴
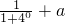=0，解得a=
，∴f（1）=-f（-1）=-（
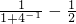）=，故答案为：
．点评：本题考查了函数奇偶性的应用，即根据奇函数的性质求值，再利用奇偶性对应的关系式，将所求的函数值的自变量的范围转化到已知范围内求解，考查了转化思想．
练习册系列答案
相关题目
设函数=f（x）在（-∞，+∞）内有定义，对于给定的正数K，定义函数fK（x）=
取函数f（x）=2-|x|．当K=
时，函数fK（x）的单调递增区间为（ ）
|
| 1 |
| 2 |
| A、（-∞，0） |
| B、（0，+∞） |
| C、（-∞，-1） |
| D、（1，+∞） |
设函数f（x）在（-∞，+∞）内有定义，对于给定的正数K，定义函数：fK（x）=
，取函数f（x）=a11（a＞1）．当K=
时，函数f（x）值域是（ ）
|
| 1 |
| a |
A、[0，
| ||
B、（0，
| ||
C、（0，1]∪[
| ||
D、（0，
|