题目内容
已知函数![]() 的图象过原点,
的图象过原点,![]() ,
, ![]() ,
,![]() ,函数
,函数![]() 与
与![]() 的图象交于不同的两点
的图象交于不同的两点![]() 、
、![]() .
.
(Ⅰ)若![]() 在
在![]() 处取得极大值
处取得极大值![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若使![]() 的
的![]() 值满足
值满足![]() ,求线段
,求线段![]() 在
在![]() 轴上的射影长
轴上的射影长![]() 的最值。
的最值。
(Ⅰ) 函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() 和
和![]() . (Ⅱ)
. (Ⅱ) ![]()
解析:
(Ⅰ)∵![]() 的图象过原点,∴
的图象过原点,∴![]() .又
.又![]() ,
,
![]() ,∴
,∴![]() ①.由
①.由![]() 在
在![]() 处取得极大值
处取得极大值![]() ,得
,得![]() ②,
②,
![]() ③.由①②③解得
③.由①②③解得![]() ,
,![]() ,
,![]() ,∴
,∴![]() …(3分)
…(3分)
由![]() ,得
,得![]() 或
或![]() .由
.由![]() ,得
,得![]() ,
,
∴函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() 和
和![]() . ……
. ……![]() 分
分
(Ⅱ)∵![]() ,∴
,∴![]() ④,
④,
![]() ⑤.由④⑤得
⑤.由④⑤得![]() .设
.设![]() ,
,![]() ,则
,则
![]() ,
,![]() .∴线段
.∴线段![]() 在
在![]() 轴上的射影长
轴上的射影长
![]() .…(8分)
.…(8分)
由![]() ,得
,得![]() .又由
.又由![]() ,得
,得![]() .……(10分)
.……(10分)
∴当![]() 时,
时,![]() 取得最大值
取得最大值![]() .当
.当![]() 时,
时,![]() 取得最大值
取得最大值![]() . ……(
. ……(![]() 分)
分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的图象过原点,且关于点(-1,1)成中心对称.
的图象过原点,且关于点(-1,1)成中心对称. ,求数列an的通项公式an.
,求数列an的通项公式an. 的图象过原点,且关于点(-1,1)成中心对称.
的图象过原点,且关于点(-1,1)成中心对称.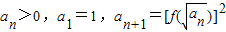 ,求数列an的通项公式an.
,求数列an的通项公式an.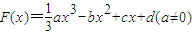 的图象过原点,f(x)=F′(x),g(x)=f′(x),f(1)=0,函数y=f(x)与y=g(x)的图象交于不同的两点A、B.
的图象过原点,f(x)=F′(x),g(x)=f′(x),f(1)=0,函数y=f(x)与y=g(x)的图象交于不同的两点A、B. ,求线段AB在x轴上的射影长的取值范围.
,求线段AB在x轴上的射影长的取值范围.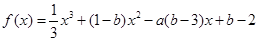 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是 ,则不等式组
,则不等式组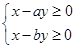 所确定的平面区域在
所确定的平面区域在 内的面积为 .
内的面积为 .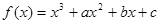 的图象过原点,且
的图象过原点,且 在
在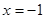 ,
, 处取得极值.
处取得极值.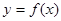 与
与 的图象有且仅有一个公共点,求实数
的图象有且仅有一个公共点,求实数 的取值范围.
的取值范围.