题目内容
已知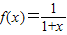 ,各项均为正数的数列{an}满足a1=1,an+2=f(an),若a2010=a2012,则a20+a11的值是( )
,各项均为正数的数列{an}满足a1=1,an+2=f(an),若a2010=a2012,则a20+a11的值是( )A.
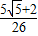
B.
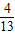
C.
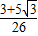
D.
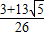
【答案】分析:先确定an+2=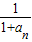 ,再分奇数项、偶数项,即可求得结论.
,再分奇数项、偶数项,即可求得结论.
解答:解:∵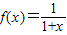 ,an+2=f(an),
,an+2=f(an),
∴an+2=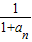
∵a1=1,∴a3= ,∴a5=
,∴a5= ,a7=
,a7= ,a9=
,a9= ,a11=
,a11=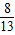 ,
,
∵a2010=a2012,∴a2010=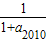 ,且偶数项均相等
,且偶数项均相等
∵a2010>0,∴a2010=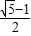 ,∴a20=
,∴a20=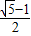 ,
,
∴a20+a11=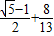 =
=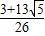
故选D.
点评:本题考查数列与函数的结合,考查学生的计算能力,解题的关键是确定an+2=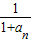 .
.
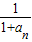 ,再分奇数项、偶数项,即可求得结论.
,再分奇数项、偶数项,即可求得结论.解答:解:∵
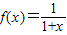 ,an+2=f(an),
,an+2=f(an),∴an+2=
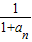
∵a1=1,∴a3=
 ,∴a5=
,∴a5= ,a7=
,a7= ,a9=
,a9= ,a11=
,a11=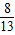 ,
,∵a2010=a2012,∴a2010=
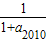 ,且偶数项均相等
,且偶数项均相等∵a2010>0,∴a2010=
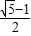 ,∴a20=
,∴a20=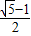 ,
,∴a20+a11=
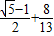 =
=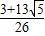
故选D.
点评:本题考查数列与函数的结合,考查学生的计算能力,解题的关键是确定an+2=
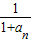 .
. 
练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 ,各项均为正数的数列
,各项均为正数的数列 满足
满足 ,若
,若 ,则
,则 .
. 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且 ,
, ;
; ,求数列
,求数列 的前
的前 项和
项和 .
.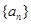 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且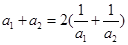 ,
,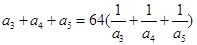
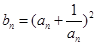 ,求数列
,求数列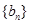 的前
的前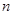 项和
项和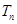 。
。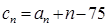 ,求数列{
,求数列{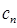 }的前
}的前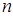 项和最小时
项和最小时 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且 ,
,
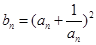 ,求数列
,求数列 的前
的前 项和
项和 。
。