题目内容
已知函数 ,则函数f(x)有两个相异零点的充要条件是
,则函数f(x)有两个相异零点的充要条件是
- A.

- B.

- C.
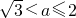
- D.-2<a<2
A
分析:令3x=t,函数f(x)有两个相异零点,等价于方程 t2-at+a2-3=0 有两个不同的正数解,等价于 ,由此求得结果.
,由此求得结果.
解答:令3x=t,则 函数 =t2-at+a2-3.
=t2-at+a2-3.
函数f(x)有两个相异零点,等价于方程 t2-at+a2-3=0 有两个不同的正数解,
等价于 ,解得
,解得  .
.
故选A.
点评:本小题主要考查指数型复合函数的性质,体现了等价转化的数学思想,属于中档题.
分析:令3x=t,函数f(x)有两个相异零点,等价于方程 t2-at+a2-3=0 有两个不同的正数解,等价于
 ,由此求得结果.
,由此求得结果.解答:令3x=t,则 函数
 =t2-at+a2-3.
=t2-at+a2-3.函数f(x)有两个相异零点,等价于方程 t2-at+a2-3=0 有两个不同的正数解,
等价于
 ,解得
,解得  .
.故选A.
点评:本小题主要考查指数型复合函数的性质,体现了等价转化的数学思想,属于中档题.

练习册系列答案
相关题目
 ,则函数f(x)的表达式为
,则函数f(x)的表达式为