题目内容
函数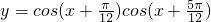 的值域为________.
的值域为________.
[- ,
, ]
]
分析:利用两角和差的余弦公式可得函数y= [
[ -sin2x],故当sin2x=1时,函数y取得最小值为-
-sin2x],故当sin2x=1时,函数y取得最小值为- ,当sin2x=-1时,函数y取得最大值为
,当sin2x=-1时,函数y取得最大值为  ,由此求得函数的值域
,由此求得函数的值域
解答:函数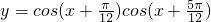 =
= [cos
[cos +cos(2x+
+cos(2x+ ]=
]= [
[ -sin2x].
-sin2x].
∴当sin2x=1时,函数y取得最小值为- ,当sin2x=-1时,函数y取得最大值为
,当sin2x=-1时,函数y取得最大值为  ,
,
故函数的值域为[- ,
, ],
],
故答案为[- ,
, ].
].
点评:本题主要考查两角和差的余弦公式的应用,正弦函数的值域,属于中档题.
 ,
, ]
]分析:利用两角和差的余弦公式可得函数y=
 [
[ -sin2x],故当sin2x=1时,函数y取得最小值为-
-sin2x],故当sin2x=1时,函数y取得最小值为- ,当sin2x=-1时,函数y取得最大值为
,当sin2x=-1时,函数y取得最大值为  ,由此求得函数的值域
,由此求得函数的值域解答:函数
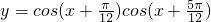 =
= [cos
[cos +cos(2x+
+cos(2x+ ]=
]= [
[ -sin2x].
-sin2x].∴当sin2x=1时,函数y取得最小值为-
 ,当sin2x=-1时,函数y取得最大值为
,当sin2x=-1时,函数y取得最大值为  ,
,故函数的值域为[-
 ,
, ],
],故答案为[-
 ,
, ].
].点评:本题主要考查两角和差的余弦公式的应用,正弦函数的值域,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 读图分析解答:设定义在闭区间[-4,4]上的函数y=f(x)的图象如图所示(图中坐标点都是实心点),完成以下几个问题:
读图分析解答:设定义在闭区间[-4,4]上的函数y=f(x)的图象如图所示(图中坐标点都是实心点),完成以下几个问题: