题目内容
5、若函数g(x)=4x+2x-2的零点在(n,n+1)之间,n∈N,则n=
0
.分析:根据函数g(x)=4x+2x-2,求出函数的单调性和零点所在的区间,再由函数g(x)=4x+2x-2的零点在(n,n+1)之间,n∈N,求出n的值.
解答:解;∵函数g(x)在[0,1]上连续且单调递增,
g(0)=1-2=-1<0,g(1)=4>0
∴函数g(x)=4x+2x-2在[0,1]上有一个零点,
又∵函数g(x)=4x+2x-2的零点在(n,n+1)之间,n∈N
∴n=0.
故答案为0.
g(0)=1-2=-1<0,g(1)=4>0
∴函数g(x)=4x+2x-2在[0,1]上有一个零点,
又∵函数g(x)=4x+2x-2的零点在(n,n+1)之间,n∈N
∴n=0.
故答案为0.
点评:考查函数零点与函数图象与x轴的交点问题,体现了转化的思想方法,属基础题.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 ,设其值域是M,
,设其值域是M,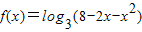 ,设其值域是M,
,设其值域是M,