Question

正方形ABCD的边长为a，MA⊥平面ABCD，且MA=a，试求：
（1）点M到BD的距离；
（2）AD到平面MBC的距离．

Answer 1

分析：（1）连接AC交BD于O，连接MO．由正方形ABCD可得BD⊥AC．由于MA⊥平面ABCD，利用三垂线定理可得MO⊥BD．于是MO为点M到BD的距离．利用勾股定理即可得出．
（2）过A作AH⊥PB于H．利用线面垂直的判定与性质可得AH⊥平面BCM．再利用线面平行的判定定理可得AD∥平面BCM．因此得到AH为AD到平面MBC的距离．

解答：解：（1）连接AC交BD于O，连接MO．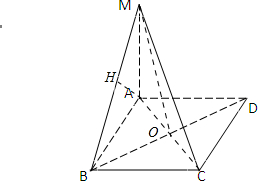
由正方形ABCD可得BD⊥AC．
∵MA⊥平面ABCD，∴MO⊥BD．
∴MO为点M到BD的距离．
∵MA=a，AO=

1

2

AC=

2

2

a，
∴MO=

MA2+AO2

=

6

2

a2．
2）过A作AH⊥PB于H．
∵MA⊥平面ABCD，BC⊥AB，
∴BC⊥AH．
∵BM∩BC=B．
∴AH⊥平面BCM．
又AD∥BC，AD?平面BCM，BC?平面BCM．
∴AD∥平面BCM．
∴AH为AD到平面MBC的距离．
在Rt△MAB中，AM=

AM2+AB2

=

2

a．
∴AH=

AM•AB

BM

=

a2

2 a

=

2

2

a．
∴AD到平面MBC的距离．

点评：本题考查了线面垂直的判定与性质、三垂线定理、线面平行的判定定理、点到直线的距离、线面的距离、勾股定理等基础知识与基本技能方法，属于中档题．