题目内容
已知函数f(x)=sinx+cosx,f′(x)是f(x)的导函数,F(x)=f(x)f′(x)+f2(x)
(Ⅰ)求F(x)的最小正周期及单调区间;
(Ⅱ)求函数F(x)在 上的值域;
上的值域;
(Ⅲ)若f(x)=2f′(x),求 的值.
的值.
(Ⅰ)求F(x)的最小正周期及单调区间;
(Ⅱ)求函数F(x)在
 上的值域;
上的值域;(Ⅲ)若f(x)=2f′(x),求
 的值.
的值.(Ⅰ)T=π.单调递增区间: 单调递减区间:
单调递减区间:
(Ⅱ)[1,1+ ];(Ⅲ)
];(Ⅲ) .
.
 单调递减区间:
单调递减区间:
(Ⅱ)[1,1+
 ];(Ⅲ)
];(Ⅲ) .
.试题分析:(I)将函数F(x)=f(x)f′(x)+f2(x)化一可得:F(x)=1+
 sin(2x+
sin(2x+ ),由此可得F(x)的最小正周期及单调区间.(Ⅱ) 由
),由此可得F(x)的最小正周期及单调区间.(Ⅱ) 由 得
得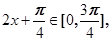 这样可得sin(2x+
这样可得sin(2x+ )的范围,从而得函数F(x)的值域.
)的范围,从而得函数F(x)的值域.(Ⅲ)由f(x)=2f′(x),得:sinx+cosx=2cosx-2sinx,由此可得tanx的值.
将
 化为只含tanx式子,将tanx.的值代入即可.
化为只含tanx式子,将tanx.的值代入即可.试题解析:(I)∵f′(x)=cosx-sinx,
∴F(x)=f(x)f′(x)+f2(x)=cos2x-sin2x+1+2sinxcosx=1+sin2x+cos2x=1+
 sin(2x+
sin(2x+ ),
),最小正周期为T=
 =π.
=π.单调递增区间:
 单调递减区间:
单调递减区间:  . 4分
. 4分(Ⅱ)由
 得
得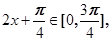
所以
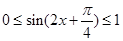 ,所以函数F(x)的值域为[1,1+
,所以函数F(x)的值域为[1,1+ ]. 8分
]. 8分(Ⅲ)∵f(x)=2f′(x), ∴sinx+cosx=2cosx-2sinx,
∴cosx=3sinx, ∴tanx=
 ,
,∴
 =
= =
= =
=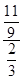 =
= . 13分
. 13分考点:1、三角变换;2、三角函数的单调性和范围;3、三角函数同角关系式.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 的前
的前 项和
项和 .
. 在区间
在区间 内的解为 .
内的解为 . ,则
,则 ( )
( ) 



 ,
, ,则
,则 的值为( )
的值为( )



 ,且
,且 ,则
,则 的值为________.
的值为________. ,则
,则 =( )
=( )



 ,则
,则 的值为( )
的值为( )



 ,
, ,则
,则 ( )
( )


