题目内容
已知函数 .
.
(1) 当 时,讨论
时,讨论 的单调性;
的单调性;
(2)设 ,当
,当 若对任意
若对任意 存在
存在 使
使 求实数
求实数 的取值范围。
的取值范围。
(1)f(x)在(0,1),(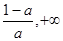 )上是增函数,在(1,
)上是增函数,在(1,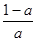 )上是减函数;(2)
)上是减函数;(2)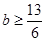 .
.
解析试题分析:(1)根据题意可以求得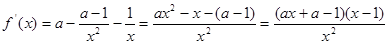 ,当
,当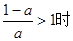 ,即
,即 时,可通过列表通过f’(x)的正负性来判断f(x)的单调性;
时,可通过列表通过f’(x)的正负性来判断f(x)的单调性;
可将 变形为
变形为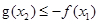 ,∴问题就等价于求当
,∴问题就等价于求当 存在
存在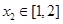 ,使
,使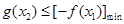 成立的b的取值范围,而
成立的b的取值范围,而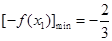 ,∴问题进一步等价于求存在
,∴问题进一步等价于求存在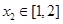 ,使
,使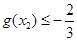 时b的取值范围,通过参变分离,可得存在
时b的取值范围,通过参变分离,可得存在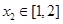 ,求使2b≥
,求使2b≥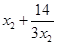 成立b的范围,∴只需2b≥
成立b的范围,∴只需2b≥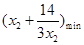 即可.
即可.
(1)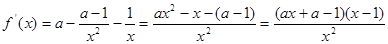 3分
3分
当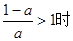 ,即
,即 时,此时f(x)的单调性如下:
时,此时f(x)的单调性如下:x (0,1) 1 (1, 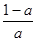 )
)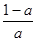
( 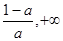 )
)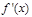
+ 0 - 0 + f(x) 增 减 增
当 时,f(x)在(0,1),(
时,f(x)在(0,1),(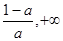 )上是增函数,在(1,
)上是增函数,在(1,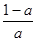 )上是减函数 7分;
)上是减函数 7分;
(2)由(1)知,当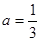 时,f(x)在(0,1)上是增函数,在(1,2)上是减函数.
时,f(x)在(0,1)上是增函数,在(1,2)上是减函数.
于是
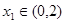 时,
时,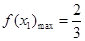

练习册系列答案
相关题目
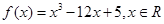 .
. 的单调区间和极值;
的单调区间和极值; 的方程
的方程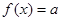 有3个不同实根,求实数a的取值范围.
有3个不同实根,求实数a的取值范围. .
. .
.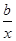 ,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0. .
. 在区间
在区间 上的最大值;
上的最大值; 存在3条直线与曲线
存在3条直线与曲线 相切,求t的取值范围;
相切,求t的取值范围; 分别存在几条直线与曲线
分别存在几条直线与曲线