题目内容
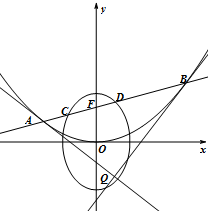 已知椭圆C1:
已知椭圆C1:| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
(Ⅰ)求C1、C2的方程;
(Ⅱ)当点Q在C1内部运动时,求△QCD面积的取值范围.
分析:(I)由椭圆条件得
,解得即可.由于抛物线的焦点F与C1的一个焦点重合,可得
=2,即可得到C2的方程.
(II)由题意知直线AB的斜率存在且过点F(0,2),令A(x1,y1)、B(x2,y2),设其方程为y=kx+2,与抛物线方联立可得根与系数的关系,由x2=8y得,y′=
x,即可得到切线AQ、BQ的方程,联立解得点Q的坐标,利用点Q在椭圆的内部可得k的取值范围.令C(x3,y3)、D(x4,y4),把直线AB的方程与椭圆方程联立可得根与系数的关系,进而得到弦长|CD|,利用点到直线的距离公式可得点Q到直线CD的距离,进而得到三角形△QCD的面积,利用导数即可得出其最值.
|
| p |
| 2 |
(II)由题意知直线AB的斜率存在且过点F(0,2),令A(x1,y1)、B(x2,y2),设其方程为y=kx+2,与抛物线方联立可得根与系数的关系,由x2=8y得,y′=
| 1 |
| 4 |
解答:解:(Ⅰ)由椭圆条件得
,解得
,
∴C1:
+
=1.
∵抛物线的焦点F与C1的一个焦点重合,
∴
=2,解得p=4,
∴C2:x2=8y.
(Ⅱ)由题意知直线AB的斜率存在且过点F(0,2),设其方程为y=kx+2,
由
消去y得,x2-8kx-16=0
令A(x1,y1)、B(x2,y2),则x1+x2=8k,x1•x2=-16,
由x2=8y得,y=
x2,y′=
x,
∴AQ:y=
x1x-
,BQ:y=
x2x-
联立AQ、BQ的方程解得,x=
=4k,y=
x2•
-
=
x1x2=-2,
∴Q(4k,-2),由于点Q在椭圆的内部,∴
+
<1,∴0≤k2<
.
由
消去y得,x2-kx-16=0,
令C(x3,y3)、D(x4,y4),则x3+x4=-
,x3•x4=-
,
∴|CD|=
=
,
Q点到直线CD的距离d=
=
,
∴△QCD的面积S△QCD=
•
•4
=
•
令
=t(1≤t<
),考察函数f(t)=
,1≤t<
,
∵f′(t)=
>0,
∴f(t)在[1,
)上单调递增,
∴f(1)≤f(t)<f(
),∴4
≤f(t)<
,
即4
≤S△QCD<
.
|
|
∴C1:
| y2 |
| 8 |
| x2 |
| 4 |
∵抛物线的焦点F与C1的一个焦点重合,
∴
| p |
| 2 |
∴C2:x2=8y.
(Ⅱ)由题意知直线AB的斜率存在且过点F(0,2),设其方程为y=kx+2,
由
|
令A(x1,y1)、B(x2,y2),则x1+x2=8k,x1•x2=-16,
由x2=8y得,y=
| 1 |
| 8 |
| 1 |
| 4 |
∴AQ:y=
| 1 |
| 4 |
| 1 |
| 8 |
| x | 2 1 |
| 1 |
| 4 |
| 1 |
| 8 |
| x | 2 2 |
联立AQ、BQ的方程解得,x=
| x1+x2 |
| 2 |
| 1 |
| 4 |
| x1+x2 |
| 2 |
| 1 |
| 8 |
| x | 2 2 |
| 1 |
| 8 |
∴Q(4k,-2),由于点Q在椭圆的内部,∴
| (-2)2 |
| 8 |
| (4k)2 |
| 4 |
| 1 |
| 8 |
由
|
令C(x3,y3)、D(x4,y4),则x3+x4=-
| 4k |
| 2+k2 |
| 4 |
| 2+k2 |
∴|CD|=
(1+k2)[(-
|
4
| ||
| k2+2 |
Q点到直线CD的距离d=
| |4k2+4| | ||
|
| k2+1 |
∴△QCD的面积S△QCD=
| 1 |
| 2 |
4
| ||
| k2+2 |
| k2+1 |
8
| ||||
| k2+2 |
令
| k2+1 |
3
| ||
| 4 |
8
| ||
| t2+1 |
3
| ||
| 4 |
∵f′(t)=
8
| ||
| (t2+1)2 |
∴f(t)在[1,
3
| ||
| 4 |
∴f(1)≤f(t)<f(
3
| ||
| 4 |
| 2 |
| 108 |
| 17 |
即4
| 2 |
| 108 |
| 17 |
点评:本题综合考查了直线与圆锥曲线的相交及相切位置关系、弦长公式、点到直线的距离公式、三角形的面积公式、利用导数研究函数的单调性及几何意义等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
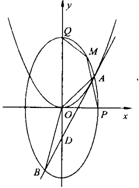 已知点D(0,-2),过点D作抛线C1:x2=2py(p>0)的切线l,切点A在第一象限,如图.
已知点D(0,-2),过点D作抛线C1:x2=2py(p>0)的切线l,切点A在第一象限,如图.