题目内容
（1）设
，求
的值；
（2）已知
，且
，求
的值．
，求的值；（2）已知
，且，求的值．（1）
；（2）
.
；（2）.试题分析：（1）将所求式分子1换成
，然后分子分母同除以
，将其转化为关于
的式子再进行计算即可，本题若由，去求出
，则需要讨论，若想不到用代替1，则可原式分子分母同除以，然后再考虑求出，显然这两种方法较为麻烦；（2）此类给三角函数值求三角函数值的问题一般是通过考察条件中的角和问题中的角的关系，然后通过诱导公式、同角三角函数关系式、和差角公式进行计算.注意到
，由诱导公式知
，结合条件由同角三角函数关系式可求出
，注意公式使用时要考察角的范围从而确定三角函数值的符号.试题解析：（1）原式=
3分
7分（2）由
，得
，故
10分而
所以
14分
练习册系列答案
相关题目
最小正周期及单调递增区间；
时，求
的最小正周期是 ．
,且
,则
的值为________.
满足
,以角
,
，以角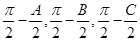
分别为内角构造一个三角形，依据正弦定理和余弦定理可以得到的等式：
.
，则
＝（ ）
，
，则
( )
，则
（ ）
