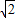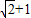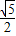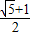题目内容
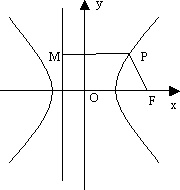
如图,F为双曲线![]() 的右焦点,P为双曲线C在第一象限内的一点,M为左准线上一点,O为坐标原点,
的右焦点,P为双曲线C在第一象限内的一点,M为左准线上一点,O为坐标原点,![]() ,
,![]() .
.
(Ⅰ)推导双曲线C的离心率e与λ的关系式;
(Ⅱ)当λ=1时,经过点(1,0)且斜率为-a的直线交双曲线于A,B两点,交y轴于点D,且![]()
![]() ,求双曲线的方程.
,求双曲线的方程.
答案:
解析:

解析:
解:
(Ⅰ)![]()
![]()
![]() 为平行四边形.
为平行四边形.
设![]() 是双曲线的右准线,且与
是双曲线的右准线,且与![]() 交于
交于![]() 点,
点,![]() ,
,
![]() ,
,![]()
![]()
即![]() 6分
6分

(Ⅱ)当![]() 时,得
时,得![]()
所以可设双曲线的方程是![]() , 8分
, 8分
设直线![]() 的方程是
的方程是![]() 与双曲线方程联立得:
与双曲线方程联立得:
![]()
由![]() 得
得![]() .
.
![]() ①
①
由已知,![]() ,因为
,因为![]()
![]() ,
,
所以可得![]() ② 10分
② 10分
由①②得![]() ,
,
消去![]() 得
得![]() 符合
符合![]() ,
,
所以双曲线的方程是![]() 14分
14分

练习册系列答案
相关题目
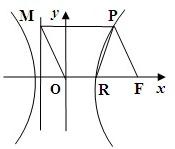 如图,F为双曲线C:
如图,F为双曲线C:
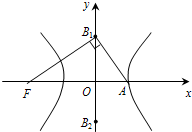 如图,F为双曲线
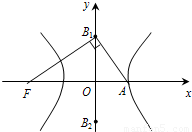
如图,F为双曲线 的左焦点,A是它的右顶点,B1B2为虚轴,若∠FB1A=90°,则双曲线的离心率是
的左焦点,A是它的右顶点,B1B2为虚轴,若∠FB1A=90°,则双曲线的离心率是



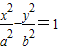 的左焦点,A是它的右顶点,B1B2为虚轴,若∠FB1A=90°,则双曲线的离心率是( )
的左焦点,A是它的右顶点,B1B2为虚轴,若∠FB1A=90°,则双曲线的离心率是( )