题目内容
设a和b都是非零实数，则不等式a＞b和
＞
同时成立的充要条件是（ ）
| 1 |
| a |
| 1 |
| b |
| A、a＞b | B、a＞b＞0 |
| C、a＞0＞b | D、0＞a＞b |
分析：根据不等式a＞b和
＞
同时成立，可得把不等式a＞b的两边同时除以ab，不等式变号，故有a＞0＞b．
| 1 |
| a |
| 1 |
| b |
解答：解：设a和b都是非零实数，∵不等式a＞b和
＞
同时成立，
∴把不等式a＞b的两边同时除以ab，不等式变号为
＜
，
∴a、b异号，∴a＞0＞b，
故选：C．
| 1 |
| a |
| 1 |
| b |
∴把不等式a＞b的两边同时除以ab，不等式变号为
| 1 |
| b |
| 1 |
| a |
∴a、b异号，∴a＞0＞b，
故选：C．
点评：本题主要考查不等式的基本性质，属于基础题．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
为纯虚数的充要条件
是非零 实数时，
恒成立
的实部和虚部都是
，若
为纯虚数的充要条件
是非零实数时，
恒成立
的实部和虚部都是
，若
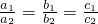是A=B的什么条件？并说明理由．