题目内容
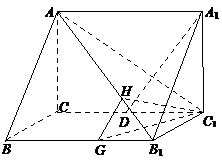
 如图所示,在直三棱柱
如图所示,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点.(Ⅰ)证明:
的中点.(Ⅰ)证明:![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅰ)略(Ⅱ)![]()
解析:
解法一:(Ⅰ)∵![]() ,∴
,∴![]() .
.
∵三棱柱![]() 为直三棱柱,∴
为直三棱柱,∴![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() ,而
,而![]() ,则
,则![]() .
.
在![]() 中,
中,![]() ,
,
 在
在![]() 中,
中,
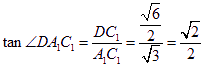 ,
,
∴![]() .
.
同理可得,![]() .
.
∵![]() ,∴
,∴![]() .即
.即![]() .
.
∵![]() ,∴
,∴![]()
![]() 平面
平面![]() . ----6分
. ----6分
(Ⅱ)如图,过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,在平面
,在平面![]() 内作
内作![]() 交
交![]() 于点
于点![]() ,连
,连![]() ,则
,则![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() ,
,![]() .
.
∵![]() ~
~![]() ,∴
,∴![]() ,则
,则![]() ,
,![]() .
.
在![]() 中,求得
中,求得![]() .
.
在![]() 中,由余弦定理,得
中,由余弦定理,得![]() .
.
 故二面角
故二面角![]() 的余弦值为
的余弦值为![]() .---13分
.---13分
解法二:∵![]() ,∴
,∴![]() .
.
∵三棱柱![]() 为直三棱柱,
为直三棱柱,
∴![]() .
.
∵![]() ,
,
∴![]() 平面
平面![]() .以
.以![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立如图所示的空间直角坐标系,则
轴建立如图所示的空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
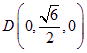 .---3分
.---3分
(Ⅰ)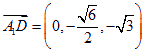 ,
,![]() ,
,![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,即
,即![]() ,
,![]() .
.
∵![]() ,∴
,∴![]()
![]() 平面
平面![]() .-------------6分
.-------------6分
(Ⅱ)设![]() 是平面
是平面![]() 的法向量,由
的法向量,由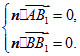 得
得
取![]() ,则
,则![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
又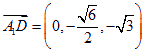 是平面
是平面![]() 的一个法向量,-----10分
的一个法向量,-----10分
且![]() 与二面角
与二面角![]() 的大小相等.
的大小相等.
由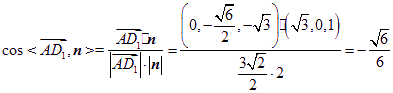 .
.
故二面角![]() 的余弦值为
的余弦值为![]() . -----------13分
. -----------13分

练习册系列答案
相关题目
 如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC,AA1=AC=BC=2,D、E、F分别是AB、AA1、CC1的中点,P是CD上的点.
如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC,AA1=AC=BC=2,D、E、F分别是AB、AA1、CC1的中点,P是CD上的点. 如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角.
如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角. 如图所示,在直三棱柱ABC-A1B1C1中,底面是∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=
如图所示,在直三棱柱ABC-A1B1C1中,底面是∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF= 如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1,AC1⊥平面A1BD,D为AC的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1,AC1⊥平面A1BD,D为AC的中点. 如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1=BC,AC1⊥平面A1BD,D为AC的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1=BC,AC1⊥平面A1BD,D为AC的中点.