题目内容
设i、j是互相垂直的单位向量,向量a=(m+1)i-3j,b=i+(m-1)j,(a+b)⊥(a-b),则实数m为( )A.-2 B.2 C.-
D.不存在
解析:(a+B)⊥(a-b),即(a+b)·(a-b)=0,a2-b2=0,|a|2-|b|2=0,而|a|2=(m+1)2+9,|b|2=1+(m-1)2,|a|2-|b|2 =m2+2m+10-(m2-2m+2)= 4m+8=0,m=-2,故选A.
答案:A
练习册系列答案
相关题目
设
，
是互相垂直的单位向量，向量
=（m+1）
-3
，
=
-（m-1）
，（
+
）⊥（
-
），则实数m为（ ）
| i |
| j |
| a |
| i |
| j |
| b |
| i |
| j |
| a |
| b |
| a |
| b |
| A、-2 | ||
| B、2 | ||
C、-
| ||
| D、不存在 |
设
，
是互相垂直的单位向量，向量
=(m+1)
-3
，
=
+(m-1)
．若(
+
)⊥(
-
)，则实数m的值是（ ）
| i |
| j |
| a |
| i |
| j |
| b |
| i |
| j |
| a |
| b |
| a |
| b |
A、-
| ||
| B、2 | ||
C、
| ||
| D、-2 |
=（m+1）
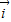-3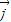
，
=
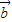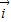-（m-1）
，（
+
）⊥（
-
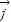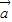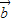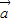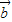），则实数m为（ ）
=（m+1）
-3
，
=
-（m-1）
，（
+
）⊥（
-
），则实数m为（ ）