题目内容
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() 且
且![]() ),且数列
),且数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列.
的等差数列.
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)若![]() ,当
,当![]() 时,求数列
时,求数列![]() 的前
的前![]() 项和
项和![]() 的最小值;
的最小值;
(3)若![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 是递增数列?若存在,求出
是递增数列?若存在,求出![]() 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
【答案】(1)证明见解析;(2)最小值为![]() ;(3)存在实数
;(3)存在实数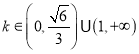 满足条件.
满足条件.
【解析】
(1)运用等差数列的通项公式和对数的定义,可得![]() ,再由等比数列的定义即可得证;
,再由等比数列的定义即可得证;
(2)求得![]() 、
、![]() ,再由等差数列和等比数列的求和公式,运用单调性即可得到最小值;
,再由等差数列和等比数列的求和公式,运用单调性即可得到最小值;
(3)由题意可得![]() 对一切
对一切![]() 成立.讨论
成立.讨论![]() ,
,![]() ,运用数列的单调性即可得到所求
,运用数列的单调性即可得到所求![]() 的范围.
的范围.
(1)由题意![]() ,即
,即![]() ,
, ![]()
![]() ,
,
![]() 常数
常数![]() 且
且![]() ,
,![]() 为非零常数,
为非零常数,
因此,数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列;
为公比的等比数列;
(2)当![]() 时,
时,![]() ,
,![]() ,
,
所以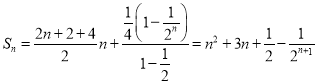 ,
,
因为![]() ,所以,
,所以,![]() 是递增数列,
是递增数列,
因而最小值为![]() ;
;
(3)由(1)知,![]() ,要使
,要使![]() 对一切
对一切![]() 成立,
成立,
即![]() 对一切
对一切![]() 成立.
成立.
当![]() 时,
时,![]() ,
,![]() 对一切
对一切![]() 恒成立;
恒成立;
当![]() 时,
时,![]() ,
,![]() 对一切
对一切![]() 恒成立,只需
恒成立,只需![]() ,
,
![]() ,所以,数列
,所以,数列![]() 单调递增,
单调递增,![]() 当
当![]() 时,
时,![]() .
.
![]() ,且
,且![]() ,
, ![]() .
.
综上所述,存在实数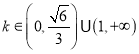 满足条件.
满足条件.

【题目】近年,国家逐步推行全新的高考制度.新高考不再分文理科,某省采用![]() 模式,其中语文、数学、外语三科为必考科目,每门科目满分均为
模式,其中语文、数学、外语三科为必考科目,每门科目满分均为![]() 分.另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物
分.另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物![]() 门科目中自选
门科目中自选![]() 门参加考试(
门参加考试(![]() 选
选![]() ),每门科目满分均为
),每门科目满分均为![]() 分.为了应对新高考,某高中从高一年级
分.为了应对新高考,某高中从高一年级![]() 名学生(其中男生
名学生(其中男生![]() 人,女生
人,女生![]() 人)中,采用分层抽样的方法从中抽取
人)中,采用分层抽样的方法从中抽取![]() 名学生进行调查,其中,女生抽取
名学生进行调查,其中,女生抽取![]() 人.
人.
(1)求![]() 的值;
的值;
(2)学校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了了解学生对这两个科目的选课情况,对抽取到的![]() 名学生进行问卷调查(假定每名学生在“物理”和“地理”这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的一个不完整的
名学生进行问卷调查(假定每名学生在“物理”和“地理”这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的一个不完整的![]() 列联表,请将下面的
列联表,请将下面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为选择科目与性别有关?说明你的理由;
的把握认为选择科目与性别有关?说明你的理由;
选择“物理” | 选择“地理” | 总计 | |
男生 |
| ||
女生 |
| ||
总计 |
(3)在抽取到的![]() 名女生中,按(2)中的选课情况进行分层抽样,从中抽出
名女生中,按(2)中的选课情况进行分层抽样,从中抽出![]() 名女生,再从这
名女生,再从这![]() 名女生中抽取
名女生中抽取![]() 人,设这
人,设这![]() 人中选择“物理”的人数为
人中选择“物理”的人数为![]() ,求
,求![]() 的分布列及期望.附:
的分布列及期望.附:![]() ,
,![]()
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |