题目内容
函数f（x）=lg（x2+1）-cosx的零点个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
分析：首先，借助于函数的零点的概念，在同一坐标系中，分别画出它们的图象，然后判断函数图象的交点个数，从而得到解决．
解答：解：令f（x）=lg（x2+1）-cosx=0，
即lg（x2+1）=cosx，
在同一坐标系中画出它们的图象如下图所示：
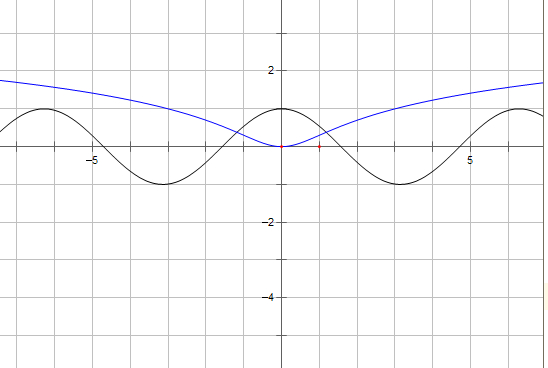
（其中蓝色曲线表示的为函数f（x）=lg（x2+1）的图象，黑色的曲线表示的为函数y=cosx的图象）
根据图象，得到两函数图象的交点个数为2个根据函数零点的定义，该函数的零点个数为2，
故选：B．
即lg（x2+1）=cosx，
在同一坐标系中画出它们的图象如下图所示：
（其中蓝色曲线表示的为函数f（x）=lg（x2+1）的图象，黑色的曲线表示的为函数y=cosx的图象）
根据图象，得到两函数图象的交点个数为2个根据函数零点的定义，该函数的零点个数为2，
故选：B．
点评：本题重点考查函数的零点的理解，注意数形结合思想在解题中的灵活运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目