题目内容
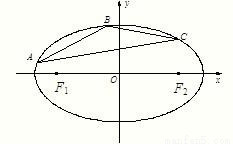
已知椭圆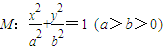 的左右焦点分别为F1(-2,0),F2(2,0).在椭圆M中有一内接三角形ABC,其顶点C的坐标
的左右焦点分别为F1(-2,0),F2(2,0).在椭圆M中有一内接三角形ABC,其顶点C的坐标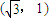 ,AB所在直线的斜率为
,AB所在直线的斜率为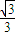 .
.(Ⅰ)求椭圆M的方程;
(Ⅱ)当△ABC的面积最大时,求直线AB的方程.
【答案】分析:(Ⅰ)由椭圆的定义知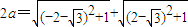 .解出a的值,再由b2=a2-c2解出b的值即可得出椭圆的方程;
.解出a的值,再由b2=a2-c2解出b的值即可得出椭圆的方程;
(II)由题意可直线AB的方程为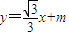 ,再由弦长公式用引入的参数m表示出弦长AB,再用m表示出点C到直线AB的距离,由三角形的面积公式将三角形的面积表示成m的函数,由基本不等式判断出面积最大时的m的值,即可求得直线AB的方程
,再由弦长公式用引入的参数m表示出弦长AB,再用m表示出点C到直线AB的距离,由三角形的面积公式将三角形的面积表示成m的函数,由基本不等式判断出面积最大时的m的值,即可求得直线AB的方程
解答:解:(Ⅰ)由椭圆的定义知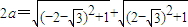 .
.
解得 a2=6,所以b2=a2-c2=2.
所以椭圆M的方程为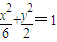 .…(4分)
.…(4分)
(Ⅱ)由题意设直线AB的方程为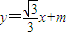 ,
,
由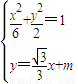 得
得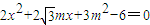 .
.
因为直线AB与椭圆M交于不同的两点A,B,且点C不在直线AB上,
所以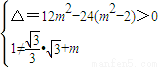 解得-2<m<2,且m≠0.
解得-2<m<2,且m≠0.
设A,B两点的坐标分别为(x1,y1),(x2,y2),
则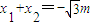 ,
,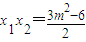 ,
,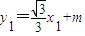 ,
,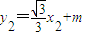 .
.
所以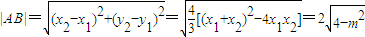 .
.
点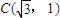 到直线
到直线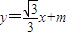 的距离
的距离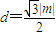 .
.
于是△ABC的面积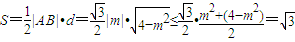 ,
,
当且仅当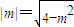 ,即
,即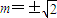 时“=”成立.
时“=”成立.
所以 时△ABC的面积最大,此时直线AB的方程为
时△ABC的面积最大,此时直线AB的方程为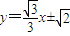 .
.
即为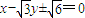 .…(13分)
.…(13分)
点评:本题考查直线与圆锥曲线的综合问题,考查了弦长的求法,三角形的面积公式,基本不等式求最值,椭圆的定义,椭圆的标准方程的求法,熟练掌握相关的知识与技巧是解题的关键,本题考查了数形结合的思想,转化的思想,对公式的记忆与灵活运用能力,是综合性较强的题目
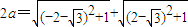 .解出a的值,再由b2=a2-c2解出b的值即可得出椭圆的方程;
.解出a的值,再由b2=a2-c2解出b的值即可得出椭圆的方程;(II)由题意可直线AB的方程为
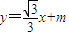 ,再由弦长公式用引入的参数m表示出弦长AB,再用m表示出点C到直线AB的距离,由三角形的面积公式将三角形的面积表示成m的函数,由基本不等式判断出面积最大时的m的值,即可求得直线AB的方程
,再由弦长公式用引入的参数m表示出弦长AB,再用m表示出点C到直线AB的距离,由三角形的面积公式将三角形的面积表示成m的函数,由基本不等式判断出面积最大时的m的值,即可求得直线AB的方程解答:解:(Ⅰ)由椭圆的定义知
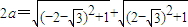 .
.解得 a2=6,所以b2=a2-c2=2.
所以椭圆M的方程为
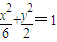 .…(4分)
.…(4分)(Ⅱ)由题意设直线AB的方程为
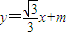 ,
,由
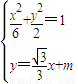 得
得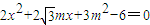 .
.因为直线AB与椭圆M交于不同的两点A,B,且点C不在直线AB上,
所以
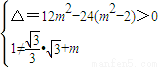 解得-2<m<2,且m≠0.
解得-2<m<2,且m≠0.设A,B两点的坐标分别为(x1,y1),(x2,y2),
则
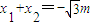 ,
,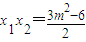 ,
,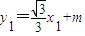 ,
,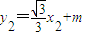 .
.所以
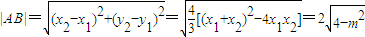 .
.点
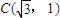 到直线
到直线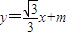 的距离
的距离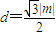 .
.于是△ABC的面积
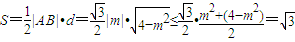 ,
,当且仅当
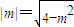 ,即
,即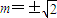 时“=”成立.
时“=”成立.所以
 时△ABC的面积最大,此时直线AB的方程为
时△ABC的面积最大,此时直线AB的方程为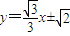 .
.即为
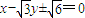 .…(13分)
.…(13分)点评:本题考查直线与圆锥曲线的综合问题,考查了弦长的求法,三角形的面积公式,基本不等式求最值,椭圆的定义,椭圆的标准方程的求法,熟练掌握相关的知识与技巧是解题的关键,本题考查了数形结合的思想,转化的思想,对公式的记忆与灵活运用能力,是综合性较强的题目

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目


 的左右焦点分别是
的左右焦点分别是 ,直线
,直线
 与椭圆
与椭圆 交于两点
交于两点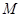 ,
, .当
.当 时,M恰为椭圆
时,M恰为椭圆 的周长为6.
的周长为6.
 与直线
与直线 分别相交于点
分别相交于点 ,
, ,问当
,问当
 为直径的圆被
为直径的圆被 轴截得的弦长是否为定值?若是,求出这个定值,
轴截得的弦长是否为定值?若是,求出这个定值, 的左右焦点分别是F1,F2,过右焦点F2且斜率为k的直线与椭圆交于A,B两点.
的左右焦点分别是F1,F2,过右焦点F2且斜率为k的直线与椭圆交于A,B两点.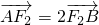 ,求k的值.
,求k的值. 已知椭圆
已知椭圆 已知椭圆
已知椭圆 已知椭圆
已知椭圆