Question

已知等腰△ABC的腰为底的2倍，则顶角A的正切值是

15

7

．

Answer 1

分析：根据题意画出相应的图形，由三角形ABC为等腰三角形，利用三线合一得到D为BC的中点，根据AB为BC的2倍，得到AB为BD的4倍，设BD=1，则有AB=4，利用勾股定理求出AD，在直角三角形ABD中，利用锐角三角函数定义求出tan∠BAD的值，由∠BAC=2∠BAD，利用二倍角的正切函数公式化简后，将tan∠BAD的值代入计算即可求出值．

解答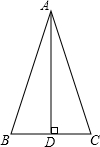：解：由题意得：AB=AC=2BC，
∵△ABC为等腰三角形，AD⊥BC，
∴D为BC的中点，∠BAD=∠CAD，
∴BD=

1

4

AB，
在Rt△ABD中，设BD=1，则AB=4，根据勾股定理得：AD=

15

，
∴tan∠BAD=

BD

AD

=

15

15

，
则tan∠BAC=tan2∠BAD=

2tan∠BAD

1-tan2∠BAD

=

2 15 15

1- 1 15

=

15

7

．
故答案为：

15

7

点评：此题考查了二倍角的正切函数公式，熟练掌握公式是解本题的关键．