题目内容
已知椭圆 的左、右顶点分别为M、N,P为椭圆上任意一点,且直线PM的斜率的取值范围是[
的左、右顶点分别为M、N,P为椭圆上任意一点,且直线PM的斜率的取值范围是[ ,2],则直线PN的斜率的取值范围是
,2],则直线PN的斜率的取值范围是
- A.
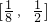
- B.
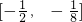
- C.[-8,-2]
- D.[2,8]
B
分析:先求出M、N的坐标,设点P的坐标,则点P的坐标满足椭圆的方程,计算直线PM的斜率与直线PN的斜率之积等于定值,求出PM的斜率取最值时,PN的斜率的值,即得PN的斜率的取值范围.
解答:M(-2,0)、N(2,0),设点P的坐标(x,y),则有 ,即 y2=1-
,即 y2=1- ,
,
直线PM的斜率与直线PN的斜率之积等于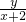 ×
×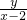 =
= =
= =-
=- ,
,
∵PM的斜率的取值范围是[ ,2],当PM的斜率等于
,2],当PM的斜率等于 时,PN的斜率等于-
时,PN的斜率等于- ,
,
当PM的斜率等于2时,PN的斜率等于- ,∴PN的斜率的取值范围为[-
,∴PN的斜率的取值范围为[- ,-
,- ],
],
故选B.
点评:本题考查椭圆的简单性质的应用,本题的关键是利用直线PM的斜率与直线PN的斜率之积等于定值.
分析:先求出M、N的坐标,设点P的坐标,则点P的坐标满足椭圆的方程,计算直线PM的斜率与直线PN的斜率之积等于定值,求出PM的斜率取最值时,PN的斜率的值,即得PN的斜率的取值范围.
解答:M(-2,0)、N(2,0),设点P的坐标(x,y),则有
 ,即 y2=1-
,即 y2=1- ,
,直线PM的斜率与直线PN的斜率之积等于
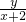 ×
×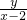 =
= =
= =-
=- ,
,∵PM的斜率的取值范围是[
 ,2],当PM的斜率等于
,2],当PM的斜率等于 时,PN的斜率等于-
时,PN的斜率等于- ,
,当PM的斜率等于2时,PN的斜率等于-
 ,∴PN的斜率的取值范围为[-
,∴PN的斜率的取值范围为[- ,-
,- ],
],故选B.
点评:本题考查椭圆的简单性质的应用,本题的关键是利用直线PM的斜率与直线PN的斜率之积等于定值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在平面直角坐标系
在平面直角坐标系 在平面直角坐标系
在平面直角坐标系 的左、右顶点分别为M、N,P为椭圆上任意一点,且直线PM的斜率的取值范围是[
的左、右顶点分别为M、N,P为椭圆上任意一点,且直线PM的斜率的取值范围是[ ,2],则直线PN的斜率的取值范围是( )
,2],则直线PN的斜率的取值范围是( ) B.
B. C.[-8,-2] D.[2,8]
C.[-8,-2] D.[2,8] 在平面直角坐标系
在平面直角坐标系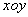 中,如图,已知椭圆
中,如图,已知椭圆 的左、右顶点为A、B,右焦点为F。设过点T(
的左、右顶点为A、B,右焦点为F。设过点T( )的直线TA、TB与椭圆分别交于点M
)的直线TA、TB与椭圆分别交于点M 、
、 ,其中m>0,
,其中m>0, 。
。 ,求点P的轨迹;
,求点P的轨迹; ,求点T的坐标;
,求点T的坐标; ,求证:直线MN必过x轴上的一定点(其坐标与m无关)。
,求证:直线MN必过x轴上的一定点(其坐标与m无关)。 本小题满分12分)
本小题满分12分) 的左、右顶点分别为
的左、右顶点分别为 曲线
曲线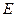 是以椭圆中心为顶点,
是以椭圆中心为顶点, 为焦点的抛物线.
为焦点的抛物线.
 与曲线
与曲线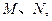 当
当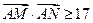 时,求直线
时,求直线 的倾斜角
的倾斜角 的取值范围.
的取值范围.