题目内容
(本题满分12分)已知四棱锥![]() 的底面为直角梯形,
的底面为直角梯形,![]() ,
,![]() ,
,
![]() 底面
底面![]() ,且
,且![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)求证:直线![]() 平面
平面![]() ;
;
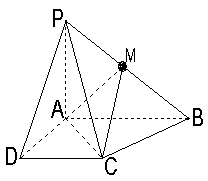 (2)若直线
(2)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的大小.
的大小.
解:方法一:(1)证明:取![]() 的中点
的中点![]() ,
,
则![]() ,故
,故![]() 平面
平面![]()
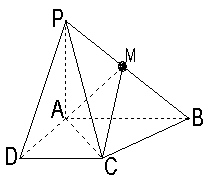 又四边形
又四边形![]() 正方形,∴
正方形,∴![]() ,故
,故![]() 平面
平面![]()
∴平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]()
![]()
(2)解:由![]() 底面
底面![]() ,得
,得![]() 底面
底面![]()
则![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
∴![]() ,
, ![]()
∴![]() 和
和![]() 都是边长为
都是边长为![]() 正三角形,取
正三角形,取![]() 的中点
的中点![]() ,则
,则![]() ,且
,且 ![]()
 ∴
∴![]() 为二面角
为二面角![]() 的平面角
的平面角![]()
在![]() 中
中 ![]() ,
,![]() ,
,
∴![]()
![]()
![]()
![]()
∴二面角![]() 的大小为
的大小为![]()
![]()
方法二:(1)设![]() ,因为
,因为![]() ,
,![]() ,
,![]() ,
,
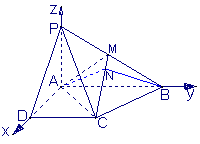
∴以A为坐标原点如图建立空间直角坐标系,![]()
取![]() 的中点
的中点![]() ,
,
则各点坐标为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
∴![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]()
∴![]() 平面
平面![]()
![]()
(2)由![]() 底面
底面![]() 及
及![]() ,得
,得![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]()
∴![]() ,
,![]()
∴![]() ,
,![]() ,
,![]() ,
,![]()
取![]() 的中点
的中点![]() , 则因
, 则因![]() ,
,![]()
∴![]()
则![]() ,且
,且 ![]() ,∴
,∴![]() 为二面角
为二面角![]() 的平面角
的平面角![]()
∵![]()
![]()
![]()
![]()
∴二面角![]() 的大小为
的大小为![]()
![]()
附:1.求出![]() 得3分;2.求法向量时公式1分,全对共2分;3.参照以上解法给分.
得3分;2.求法向量时公式1分,全对共2分;3.参照以上解法给分.

练习册系列答案
相关题目
 的三个内角
的三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 .
. ,且
,且 .(1)求
.(1)求 .求
.求 .
. ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 :
: 的长轴长是短轴长的
的长轴长是短轴长的 倍,
倍, ,
, 是它的左,右焦点.
是它的左,右焦点. ,且
,且 ,
, ,求
,求 作以
作以 (
( 是切点),且使
是切点),且使 ,求动点
,求动点 的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量
的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量 与
与 是共线向量
是共线向量 分别是左右焦点,求
分别是左右焦点,求 的取值范围
的取值范围