题目内容
在平面直角坐标系xOy中,将点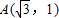 绕原点O逆时针旋转90°到点B,那么点B坐标为 ,若直线OB的倾斜角为α,则tan2α= .
绕原点O逆时针旋转90°到点B,那么点B坐标为 ,若直线OB的倾斜角为α,则tan2α= .
【答案】分析:可设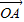 =
=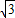 +i,
+i,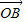 =
=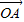 •i,从而可求得点B的坐标,由tanα=-
•i,从而可求得点B的坐标,由tanα=-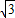 ,利用二倍角的正切可求tan2α.
,利用二倍角的正切可求tan2α.
解答:解:设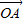 =
=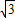 +i,∵点A(
+i,∵点A(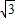 ,1)绕原点O逆时针旋转90°到点B,
,1)绕原点O逆时针旋转90°到点B,
∴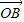 =
=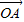 •i=(
•i=(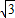 +i)•i=-1+
+i)•i=-1+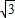 i,
i,
∴点B坐标为(-1,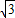 );
);
∵直线OB的倾斜角为α,
∴tanα=-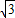 ,
,
∴tan2α=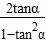 =
=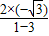 =
=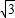 .
.
故答案为:(-1,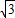 );
);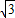 .
.
点评:本题考查复数的乘法的几何意义,考查二倍角的正切,考查转化思想与方程思想的综合应用,属于中档题.
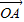 =
=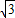 +i,
+i,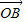 =
=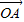 •i,从而可求得点B的坐标,由tanα=-
•i,从而可求得点B的坐标,由tanα=-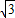 ,利用二倍角的正切可求tan2α.
,利用二倍角的正切可求tan2α.解答:解:设
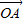 =
=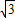 +i,∵点A(
+i,∵点A(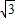 ,1)绕原点O逆时针旋转90°到点B,
,1)绕原点O逆时针旋转90°到点B,∴
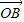 =
=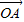 •i=(
•i=(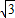 +i)•i=-1+
+i)•i=-1+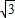 i,
i,∴点B坐标为(-1,
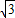 );
);∵直线OB的倾斜角为α,
∴tanα=-
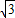 ,
,∴tan2α=
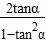 =
=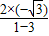 =
=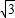 .
.故答案为:(-1,
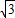 );
);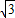 .
.点评:本题考查复数的乘法的几何意义,考查二倍角的正切,考查转化思想与方程思想的综合应用,属于中档题.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是