题目内容
已知函数![]() .(Ⅰ)分别求函数
.(Ⅰ)分别求函数![]() 和
和![]() 的图象在
的图象在![]() 处的切线方程;(Ⅱ)证明不等式
处的切线方程;(Ⅱ)证明不等式![]() ;(Ⅲ)对一个实数集合
;(Ⅲ)对一个实数集合![]() ,若存在实数
,若存在实数![]() ,使得
,使得![]() 中任何数都不超过
中任何数都不超过![]() ,则称
,则称![]() 是
是![]() 的一个上界.已知
的一个上界.已知![]() 是无穷数列
是无穷数列![]() 所有项组成的集合的上界(其中
所有项组成的集合的上界(其中![]() 是自然对数的底数),求实数
是自然对数的底数),求实数![]() 的最大值.
的最大值.
【解析】:(Ⅰ)![]() ,则
,则![]() ,且
,且
![]() ,所以函数
,所以函数![]() 和
和![]() 的图象在
的图象在![]() 处的切线方程都是
处的切线方程都是![]() ……3分
……3分
(Ⅱ)令函数![]() ,定义域是
,定义域是![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数,
上为增函数,

 ,设
,设![]() ,则
,则
![]() ………10分
………10分
由(Ⅱ)知,![]() ,即
,即![]() ,
,
所以![]() ,于是
,于是![]() 在
在![]() 上为减函数.
上为减函数.
故函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,所以
,所以![]() 的最大值为
的最大值为![]() ………13分
………13分

练习册系列答案
相关题目
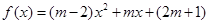 的两个零点分别在区间
的两个零点分别在区间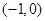 和区间
和区间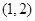 内,则实数
内,则实数 的取值范围是 ( )
的取值范围是 ( )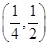 B.
B.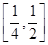 C.
C.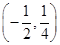 D.
D.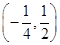
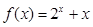 ,
,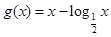 ,
,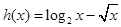 的零点分别为
的零点分别为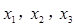 ,则
,则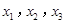 的大小关系是( )
的大小关系是( )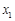 >
>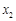 >
>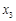 B.
B. ,
, ,
, 的零点分别为
的零点分别为
 ,则
,则 的大小关系是(
)]
的大小关系是(
)] B
B 
 D
D 
 定义域内任意的两个自变量的值
定义域内任意的两个自变量的值 ,当
,当 时,都有
时,都有 ,且存在两个不相等的自变量值
,且存在两个不相等的自变量值 ,使得
,使得 ,就称
,就称 的定义域、值域分别为
的定义域、值域分别为 、
、 ,
, ,
, ,
且
,
且