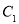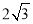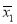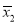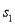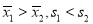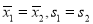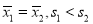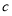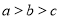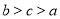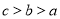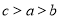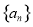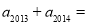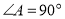题目内容
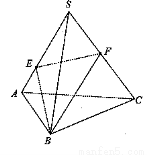
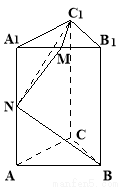
如图,直三棱柱(侧棱垂直于底面的棱柱)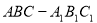 ,底面
,底面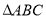 中
中 ,棱
,棱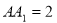 ,
,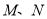 分别为
分别为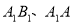 的中点.
的中点.
(1)求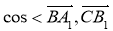 >的值;
>的值;
(2)求证:
(1)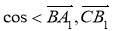 >的值为
>的值为 ;(2)证明过程详见试题解析.
;(2)证明过程详见试题解析.
【解析】
试题分析:(1)先以C为原点建立空间坐标系,由已知易求出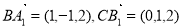 ,进而可求
,进而可求 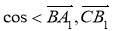 >的值;
>的值;
(2)由(1)所建立的空间坐标系可写出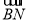 、
、 、
、 的坐标表示,即可知
的坐标表示,即可知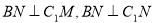 ,从而
,从而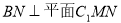 得证.
得证.
试题解析:以C为原点,CA、CB、CC1所在的直线分别为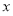 轴、
轴、 轴、
轴、 轴,建立坐标系
轴,建立坐标系
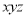
(1)依题意得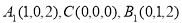 ,∴
,∴ 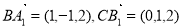
∴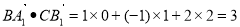
 ,
,
∴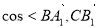 >=
>= 6分
6分
(2) 依题意得 ∴
∴  ,
,
∴ 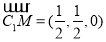 ,
,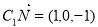 ,
,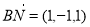
∴ 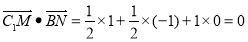 ,
,
∴ 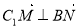 ,
,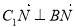 ∴
∴ 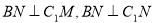
∴ 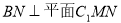 12分
12分
考点:空间坐标系、线面垂直的判定方法.

练习册系列答案
相关题目
在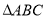 中,
中,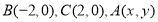 ,给出
,给出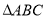 满足的条件,就能得到动点
满足的条件,就能得到动点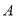 的轨迹方程,下表给出了一些条件及方程:
的轨迹方程,下表给出了一些条件及方程:
条件 | 方程 |
① |
|
② |
|
③ |
|
则满足条件①、②、③的点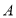 轨迹方程按顺序分别是
轨迹方程按顺序分别是
A. 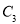 、
、 、
、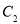 B.
B. 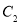 、
、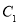 、
、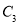
C. 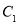 、
、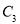 、
、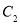 D.
D. 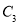 、
、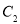 、
、