题目内容
已知P是正方形ABCD平面外一点，M、N分别是PA、BD上的点，且PM∶MA=BN∶ND=5∶8.求证：直线MN∥平面PBC.
证明：
=
+
+
=-
+
+
=-
+
+
=-
(
-
)+
+
(
+
)
=
-
+
=
-
=
(
-
).
在BC上取点E，使BE=
,于是
=
(
-
)= 
.
∴MN∥PE.?
∵MN平面PBC,?
∴MN∥平面PBC.?
温馨提示：用向量知识解题，一般不需要作辅助线，只是利用向量运算及基本定理，把要证的向量用该平面内的向量表示.
练习册系列答案
相关题目
如图，已知四棱锥P--ABC的底面ABCD为正方形，PA⊥平面ABCD，PA=AB=2，e为PC的中点，F为AD的中点．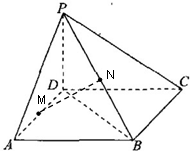
已知四棱锥P-ABCD的底面ABCD是正方形，M，N分别为AD，PB的中点，且PD⊥底面ABCD，其中PD=AD=a．
如图，在三棱柱ABC-A1B1C1中，侧面ABB1A，ACC1A1均为正方形，∠BAC=90°，AB=2，点D1是棱B1C1的中点．