题目内容
已知向量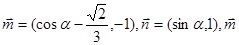 与
与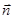 为共线向量,且
为共线向量,且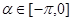 .
.
(1)求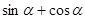 的值;
的值;
(2)求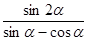 的值.
的值.
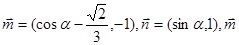 与
与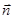 为共线向量,且
为共线向量,且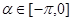 .
.(1)求
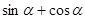 的值;
的值;(2)求
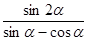 的值.
的值.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)先利用向量
 列式求解
列式求解 的值;(2)在(1)的条件下利用平方关系
的值;(2)在(1)的条件下利用平方关系 先求出
先求出 的值,然后计算
的值,然后计算 的值,根据角
的值,根据角 的取值范围确定
的取值范围确定 的正负,进而求出
的正负,进而求出 的值,最后代数求解相应的值即可.
的值,最后代数求解相应的值即可.试题解析:(1)
 ,
, ,且
,且 ,
,所以
 ,整理得
,整理得 ;
;(2)由(1)知,
 ,平方得
,平方得 ,
,即
 ,即
,即 ,
,而
 ,
, ,
, ,
, ,所以
,所以 ,故
,故 ,
,所以
 ,所以
,所以 .
.
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 ;
; ;
; ;
; ;
; .
. .
. 的单调递增区间;
的单调递增区间; ,求
,求 的值
的值 中,
中, 分别是
分别是 的对边,
的对边, ,
, ,
, ,
, .
. 的值;
的值; 的值.
的值.  ,则函数
,则函数 的最小正周期为( )
的最小正周期为( )
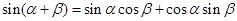 ------①
------①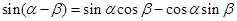 ------②
------②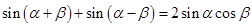 ------③
------③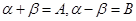 有
有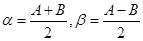
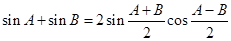 .
. ;
;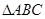 的三个内角
的三个内角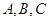 满足
满足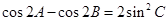 ,试判断
,试判断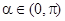 ,且
,且 ,则
,则 的值为( )
的值为( )

 且
且 则
则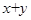 的可能取值是( )
的可能取值是( ) B
B 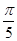 C.
C.  D.
D. 