题目内容
已知:在直角坐标系xOy中,曲线C的参数方程为:
(t为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系.求曲线C的极坐标方程.
|
分析:将曲线C的参数方程中的两式相除得到
=
,代入x=
化简得x2+y2-2x=0(x>0).再由直角坐标与极坐标互化的公式,将(ρcosθ,ρsinθ)代入前面的方程,化简即可得到曲线C的极坐标方程.
| t |
| y |
| x |
| 2 |
| 1+t |
解答:解:∵
,得t≥0,
∴0<x≤2,
两式相除,得
=
,
代入x=
得C:x2+y2-2x=0(x>0)①,
又∵极坐标中x=ρcosθ,y=ρsinθ,
∴将(ρcosθ,ρsinθ)代入①,得ρ2cos2θ+ρ2sin2θ-2ρcosθ=0,
化简得ρ=2cosθ(ρ>0),即为曲线C的极坐标方程.
|
∴0<x≤2,
两式相除,得
| t |
| y |
| x |
代入x=
| 2 |
| 1+t |
又∵极坐标中x=ρcosθ,y=ρsinθ,
∴将(ρcosθ,ρsinθ)代入①,得ρ2cos2θ+ρ2sin2θ-2ρcosθ=0,
化简得ρ=2cosθ(ρ>0),即为曲线C的极坐标方程.
点评:本题给出曲线C的参数方程,求曲线C的极坐标方程.着重考查了曲线的参数方程、直角坐标方程与坐标方程及其相互转化的知识,属于中档题.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
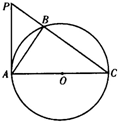 (二)选择题(考生在A、B、C三小题中选做一题,多做按所做第一题评分)
(二)选择题(考生在A、B、C三小题中选做一题,多做按所做第一题评分)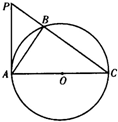 (二)选择题(考生在A、B、C三小题中选做一题,多做按所做第一题评分)
(二)选择题(考生在A、B、C三小题中选做一题,多做按所做第一题评分)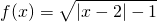 的定义域为________
的定义域为________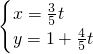 (t为参数).则曲线C上的点到直线l的最短距离为________.
(t为参数).则曲线C上的点到直线l的最短距离为________. 的定义域为
的定义域为  (t为参数).则曲线C上的点到直线l的最短距离为 .
(t为参数).则曲线C上的点到直线l的最短距离为 .